题目内容
10.在△ABC中,点D在AB边上,AD=CD,DE⊥AC于点E,CF∥AB,交DE的延长线于点F.(1)如图1,求证:四边形ADCF是菱形;
(2)如图2,当∠ACB=90°,∠B=30°时,在不添加辅助线的情况下,请直接写出图中与线段AC相等的线段(线段AC除外).

分析 (1)如图1,利用等腰三角形的性质得∠DCA=∠ADC,CE=AE,再利用CF∥AB得到∠ECF=∠EAD,则∠DCA=∠ECF,于是根据等腰三角形的判定方法可得AD=CF,所以四边形ADCF为平行四边形,
加上DA=DC可判断四边形ADCF是菱形;
(2)如图2,先证明△ADC为等边三角形得到AC=AD=CD,∠ACD=60°,再利用菱形的性质可得AC=AD=DC=CF=AF,然后证明BD=CD即可.
解答 解:(1)证明:如图1,
∵AD=CD,DE⊥AC,
∴∠DCA=∠ADC,CE=AE,
∵CF∥AB,
∴∠ECF=∠EAD,
∴∠DCA=∠ECF,
即CE平分∠DCF,
而CE⊥DF,
∴CD=CF,
∴AD=CF,
∴AD∥CF,
∴四边形ADCF为平行四边形,
而DA=DC,
∴四边形ADCF是菱形;
(2)如图2,∵∠ACB=90°,∠B=30°,
∴∠BAC=60°,
而DA=DC,
∴△ADC为等边三角形,
∴AC=AD=CD,∠ACD=60°,
∵四边形ADCF为菱形,
∴AC=AD=DC=CF=AF,
∵∠B=∠DCB=30°,
∴BD=CD,
∴AC=AD=DC=CF=AF=BD.
点评 本题考查了菱形的判定与性质:菱形的中点四边形是矩形(对角线互相垂直的四边形的中点四边形定为矩形,对角线相等的四边形的中点四边形定为菱形).;菱形是在平行四边形的前提下定义的,首先它是平行四边形,但它是特殊的平行四边形,特殊之处就是“有一组邻边相等”,因而就增加了一些特殊的性质和不同于平行四边形的判定方法.

练习册系列答案
相关题目
18.单项式-52xy3的次数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
5.反比例函数y=$\frac{2-3k}{x}$的图象经过点(-2,5),则k的值为( )
| A. | 10 | B. | -10 | C. | 4 | D. | -4 |
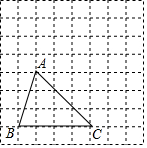 三角形ABC在正方形网格中的位置如图所示,网格中每个小方格的边长为1个单位长度,请根据下列提示作图
三角形ABC在正方形网格中的位置如图所示,网格中每个小方格的边长为1个单位长度,请根据下列提示作图