Question

10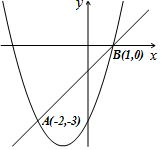．如图，二次函数y=ax²+bx+c（a≠0）和一次函数y=x-1的图象交于A（-2，-3）、B（1，0）两点，则方程ax²+（b-1）x+c+1=0的根为（　　）

• A． x₁=-2，x₂=-3
• B． x₁=1，x₂=0
• C． x₁=-2，x₂=1
• D． x₁=-3，x₂=0

Answer 1

分析 将方程ax²+（b-1）x+c+1=0，变形为ax²+bx+c=x-1，则原问题可转化为二次函数y=ax²+bx+c（a≠0）和一次函数y=x-1的图象交点的横坐标，结合函数图象解答即可．

解答 解：
∵ax²+（b-1）x+c+1=0，
∴ax²+bx+c=x-1，
∴方程ax²+（b-1）x+c+1=0的根即为二次函数y=ax²+bx+c（a≠0）和一次函数y=x-1的图象交点的横坐标，
∵二次函数y=ax²+bx+c（a≠0）和一次函数y=x-1的图象交于A（-2，-3）、B（1，0）两点，
∴方程ax²+（b-1）x+c+1=0的根为x₁=-2，x₂=1，
故选C．

点评 本题考查了二次函数的性质，主要利用了函数图象的交点坐标与方程组，体现了利用函数思想解方程组和利用方程的思想解函数的问题．