题目内容
观察多项式mx+my+nx+ny,它的各项并没有公因式,也不能直接用公式法分解,那么通过观察发现,前两项有公因式m,后两项有公因式n,这样就把多项式分成两组,得到 m(x+y)+n(x+y),这样就会发现又有新的公因式(x+y),就可完成分解因式.分解的过程是:
mx+my+nx+ny=(mx+my)+(nx+ny)=m(x+y)+n(x+y)=(m+n)(x+y)
像这样把一个多项式进行分组来进行分解因式的方法叫做分组分解法,根据上面的例题来进行下列因式分解.
(1)a2-b2-a-b;
(2)4x2-4x-y2+1.
mx+my+nx+ny=(mx+my)+(nx+ny)=m(x+y)+n(x+y)=(m+n)(x+y)
像这样把一个多项式进行分组来进行分解因式的方法叫做分组分解法,根据上面的例题来进行下列因式分解.
(1)a2-b2-a-b;
(2)4x2-4x-y2+1.
考点:因式分解-分组分解法
专题:阅读型
分析:(1)首先将前两项利用平方差公式分解因式,进而提取公因式得出即可;
(2)将4x2-4x+1利用完全平方公式分解因式,进而利用平方差公式分解因式得出即可.
(2)将4x2-4x+1利用完全平方公式分解因式,进而利用平方差公式分解因式得出即可.
解答:解:(1)a2-b2-a-b
=(a+b)(a-b)-(a+b)
=(a+b)(a-b-1);
(2)4x2-4x-y2+1
=(2x-1)2-y2
=(2x-1-y)(2x-1+y).
=(a+b)(a-b)-(a+b)
=(a+b)(a-b-1);
(2)4x2-4x-y2+1
=(2x-1)2-y2
=(2x-1-y)(2x-1+y).
点评:此题主要考查了分组分解法因式分解,正确分组得出是解题关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
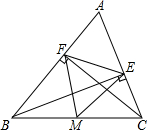 如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点.
如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点.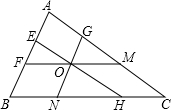 已知O是△ABC内一点,且GN∥AB,FM∥BC,EH∥AC,求证:
已知O是△ABC内一点,且GN∥AB,FM∥BC,EH∥AC,求证: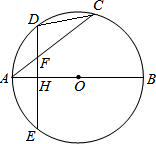 如图,已知AB、AC分别为⊙O的直径和弦,D为
如图,已知AB、AC分别为⊙O的直径和弦,D为
 正方形ABCD的边长为4,请你建立适当的平面直角坐标系,写出各个顶点的坐标.
正方形ABCD的边长为4,请你建立适当的平面直角坐标系,写出各个顶点的坐标.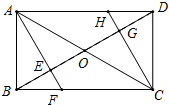 如图,矩形ABCD中,O是两条对角线的交点,AF垂直平分线段OB,垂足为E,CH垂直平分线段OD,垂足为G.求证:
如图,矩形ABCD中,O是两条对角线的交点,AF垂直平分线段OB,垂足为E,CH垂直平分线段OD,垂足为G.求证: 已知在△ABC中,∠B=∠C,BD=CE,求证:DE∥BC.
已知在△ABC中,∠B=∠C,BD=CE,求证:DE∥BC.