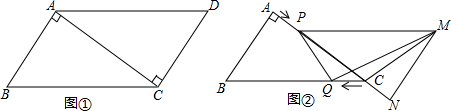
题目内容
3.如图1,P点从点A开始以2厘米/秒的速度沿A→B→C的方向移动,点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动,在直角三角形ABC中,∠A=90°,若AB=16厘米,AC=12厘米,BC=20厘米,如果P、Q同时出发,用t(秒)表示移动时间,那么:(1)如图1,若P在线段AB上运动,Q在线段CA上运动,试求出t为何值时,QA=AP
(2)如图2,点Q在CA上运动,试求出t为何值时,三角形QAB的面积等于三角形ABC面积的$\frac{1}{4}$;
(3)如图3,当P点到达C点时,P、Q两点都停止运动,试求当t为何值时,线段AQ的长度等于线段BP的长的$\frac{1}{4}$

分析 (1)当P在线段AB上运动,Q在线段CA上运动时,设CQ=t,AP=2t,则AQ=12-t,由AQ=AP,可得方程12-t=2t,解方程即可.
(2)当Q在线段CA上时,设CQ=t,则AQ=12-t,根据三角形QAB的面积等于三角形ABC面积的$\frac{1}{4}$,列出方程即可解决问题.
(3)分三种情形讨论即可①当0<t≤8时,P在线段AB上运动,Q在线段CA上运动.②当8<t≤12时,Q在线段CA上运动,P在线段BC上运动.③当t>12时,Q在线段AB上运动,P在线段BC上运动时,分别列出方程求解即可.
解答 解:(1)当P在线段AB上运动,Q在线段CA上运动时,设CQ=t,AP=2t,则AQ=12-t,
∵AQ=AP,
∴12-t=2t,
∴t=4.
∴t=4s时,AQ=AP.
(2)当Q在线段CA上时,设CQ=t,则AQ=12-t,
∵三角形QAB的面积等于三角形ABC面积的$\frac{1}{4}$,
∴$\frac{1}{2}$•AB•AQ=$\frac{1}{4}$×$\frac{1}{2}$•AB•AC,
∴$\frac{1}{2}$×16×(12-t)=$\frac{1}{8}$×16×12,解得t=9.
∴t=9s时,三角形QAB的面积等于三角形ABC面积的$\frac{1}{4}$.
(3)由题意可知,Q在线段CA上运动的时间为12秒,P在线段AB上运动时间为8秒,
①当0<t≤8时,P在线段AB上运动,Q在线段CA上运动,设CQ=t,AP=2t,则AQ=12-t,BP=16-2t,
∵AQ=$\frac{1}{4}$BP,
∴12-t=$\frac{1}{4}$(16-2t),解得t=16(不合题意舍弃).
②当8<t≤12时,Q在线段CA上运动,P在线段BC上运动,设CQ=t,则AQ=12-t,BP=2t-16,
∵AQ=$\frac{1}{4}$BP,
∴12-t=$\frac{1}{4}$(2t-16),解得t=$\frac{32}{3}$.
③当t>12时,Q在线段AB上运动,P在线段BC上运动时,
∵AQ=t-12,BP=2t-16,
∵AQ=$\frac{1}{4}$BP,
∴t-12=$\frac{1}{4}$(2t-16),解得t=16,
综上所述,t=$\frac{32}{3}$s或16s时,AQ=$\frac{1}{4}$BP.
点评 本题考查三角形综合题,三角形面积、一元一次方程等知识,解题的关键是理解题意,学会用方程的思想思考问题,属于中考常考题型.

 如图,若有理数a、b在数轴上的对应点的位置如图所示,则下列各式错误的是( )
如图,若有理数a、b在数轴上的对应点的位置如图所示,则下列各式错误的是( )| A. | $\frac{|a|}{a}$+$\frac{|b|}{b}$=0 | B. | a+b<0 | C. | |a+b|-a=b | D. | -b<a<-a<b |
 如图,把“QQ”笑脸放在直角坐标系中,已知右眼A的坐标是(-2,3),嘴唇C点的坐标为(-1,1),则此“QQ”笑脸左眼B的坐标是( )
如图,把“QQ”笑脸放在直角坐标系中,已知右眼A的坐标是(-2,3),嘴唇C点的坐标为(-1,1),则此“QQ”笑脸左眼B的坐标是( )| A. | (0,3) | B. | (0,1) | C. | (-1,2) | D. | (-1,3) |
 如图,能用图中字母表示出来的不同射线共有( )
如图,能用图中字母表示出来的不同射线共有( )| A. | 3条 | B. | 4条 | C. | 6条 | D. | 8条 |
 如图,身高1.6米的小明站在距离路灯的底部(点O)20米的A处,测得小明的影子AM长为4米,则路灯距离地面9.6米.
如图,身高1.6米的小明站在距离路灯的底部(点O)20米的A处,测得小明的影子AM长为4米,则路灯距离地面9.6米. 如图,已知线段AB=8cm,延长线段AB到C,使BC=2AB,点D是AC的中点,则BD等于4cm.
如图,已知线段AB=8cm,延长线段AB到C,使BC=2AB,点D是AC的中点,则BD等于4cm. 如图,在直角△ABC中,斜边AB上的垂直平分线交直角边BC于D,交AB于E,若BC=10cm,AC=6cm,则△ADC的周长为16cm.
如图,在直角△ABC中,斜边AB上的垂直平分线交直角边BC于D,交AB于E,若BC=10cm,AC=6cm,则△ADC的周长为16cm.