题目内容
?ABCD中,AC=4,BD=8,则边AB的范围
- A.AB>4
- B.AB<12
- C.AB>0
- D.2<AB<6
D
分析:解答此题的关键是连接AC、BD,利用平行四边形的性质求出AO和BO的长,然后利用三角形三边关系进行求解.
解答: 解:连接AC、BD,两对角线相交于一点O,
解:连接AC、BD,两对角线相交于一点O,
∵?ABCD中∴AC,BD互相平分,
AO=OC=2,BO=OD=4,
∴在△ABO中,由三角形三边关系得
AO+BO>AB,BO-AO<AB
则边AB的范围:2<AB<6.
故选D.
点评:此题主要考查学生对平行四边形的性质和三角形三边关系的理解和掌握,解答此题的关键是连接AC、BD,利用平行四边形的性质求出AO和BO的长,此题属于中档题.
分析:解答此题的关键是连接AC、BD,利用平行四边形的性质求出AO和BO的长,然后利用三角形三边关系进行求解.
解答:
 解:连接AC、BD,两对角线相交于一点O,
解:连接AC、BD,两对角线相交于一点O,∵?ABCD中∴AC,BD互相平分,
AO=OC=2,BO=OD=4,
∴在△ABO中,由三角形三边关系得
AO+BO>AB,BO-AO<AB
则边AB的范围:2<AB<6.
故选D.
点评:此题主要考查学生对平行四边形的性质和三角形三边关系的理解和掌握,解答此题的关键是连接AC、BD,利用平行四边形的性质求出AO和BO的长,此题属于中档题.

练习册系列答案
相关题目
 16、如图,在四边形ABCD中,AC⊥BD,依次连接四边形ABCD各边的中点所得到的四边形为( )
16、如图,在四边形ABCD中,AC⊥BD,依次连接四边形ABCD各边的中点所得到的四边形为( )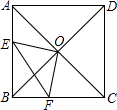 正方形ABCD中,AC、BD交于O,∠EOF=90°,已知AE=3,CF=4,则EF的长为
正方形ABCD中,AC、BD交于O,∠EOF=90°,已知AE=3,CF=4,则EF的长为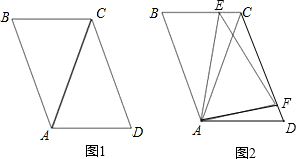 如图1,在平行四边形ABCD中,AC=CD.
如图1,在平行四边形ABCD中,AC=CD. 如图,在四边形ABCD中,AC是∠DAE的平分线,DA∥CE,∠AEB=∠CEB.求证:AB=CB.
如图,在四边形ABCD中,AC是∠DAE的平分线,DA∥CE,∠AEB=∠CEB.求证:AB=CB. 10、如图,在菱形ABCD中,AC与BD相交于O,P是AB上一点,PO=PA=3,则菱形ABCD的周长是
10、如图,在菱形ABCD中,AC与BD相交于O,P是AB上一点,PO=PA=3,则菱形ABCD的周长是