题目内容
19.(1)计算($\frac{1}{4}$)-1-$\sqrt{27}$+(5-π)0+6tan60°(2)求不等式组$\left\{\begin{array}{l}2(x-2)≤4x-3\\ 2x-5<1-x\end{array}$的整数解.
分析 (1)原式第一项利用负整数指数幂法则计算,第二项利用立方根定义计算,第三项利用零指数幂法则计算,最后一项利用特殊角的三角函数值计算即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分,确定出整数解即可.
解答 解:(1)原式=4-3$\sqrt{3}$+1+6$\sqrt{3}$=5+3$\sqrt{3}$;
(2)$\left\{\begin{array}{l}{2(x-2)≤4x-3①}\\{2x-5<1-x②}\end{array}\right.$,
由①得:x≥-$\frac{1}{2}$,
由②得:x<2,
故不等式的解集为-$\frac{1}{2}$≤x<2;
则不等式的整数解为x=0,1.
点评 此题考查了实数的运算,以及一元一次不等式组的整数解,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
10.下列命题的逆命题正确的是( )
| A. | 对顶角相等 | |
| B. | 三边相等的三角形是等边三角形 | |
| C. | 如果一个四边形是正方形,那么它的四条边相等 | |
| D. | 如果一个四边形是矩形,那么它的对角线相等 |
14.某校对各个班级教室卫生情况的考评包括以下几项:门窗,桌椅,地面,一天,两个班级的各项卫生成绩分别如表:(单位:分)
(1)两个班的平均得分分别是多少;
(2)按学校的考评要求,将黑板、门窗、桌椅、地面这三项得分依次按25%、35%、40%的比例计算各班的卫生成绩,那么哪个班的卫生成绩高?请说明理由.
| 门窗 | 桌椅 | 地面 | |
| 一班 | 85 | 90 | 95 |
| 二班 | 95 | 85 | 90 |
(2)按学校的考评要求,将黑板、门窗、桌椅、地面这三项得分依次按25%、35%、40%的比例计算各班的卫生成绩,那么哪个班的卫生成绩高?请说明理由.
11. 如图是小鹏自己制作的正方形飞镖盘,并在盘内画了两个小正方形,则小鹏在投掷飞镖时,飞镖扎在阴影部分的概率为( )
如图是小鹏自己制作的正方形飞镖盘,并在盘内画了两个小正方形,则小鹏在投掷飞镖时,飞镖扎在阴影部分的概率为( )
 如图是小鹏自己制作的正方形飞镖盘,并在盘内画了两个小正方形,则小鹏在投掷飞镖时,飞镖扎在阴影部分的概率为( )
如图是小鹏自己制作的正方形飞镖盘,并在盘内画了两个小正方形,则小鹏在投掷飞镖时,飞镖扎在阴影部分的概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{3}$ |
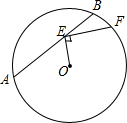 如图,已知⊙O的半径为5,弦AB=8,点E在AB上运动,连结OE,过点E作EF⊥OE交⊙O于点F,当EF最大时,OE+EF的值为7.
如图,已知⊙O的半径为5,弦AB=8,点E在AB上运动,连结OE,过点E作EF⊥OE交⊙O于点F,当EF最大时,OE+EF的值为7.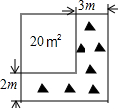 如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地,则原正方形空地的边长是( )
如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了2m,另一边减少了3m,剩余一块面积为20m2的矩形空地,则原正方形空地的边长是( )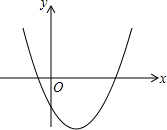 在二次函数y=ax2+bx+c的图象如图所示,下列说法中:①b2-4ac<0;②$-\frac{b}{2a}$>0;③abc>0;④a-b-c>0,说法正确的是②③④(填序号).
在二次函数y=ax2+bx+c的图象如图所示,下列说法中:①b2-4ac<0;②$-\frac{b}{2a}$>0;③abc>0;④a-b-c>0,说法正确的是②③④(填序号).