题目内容
20. 如图,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.
如图,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.(1)△ABC的形状是等边三角形;(直接填空,不必说理)
(2)延长BP到D点,使得BD=CP,连接AD,试判断△ADP的形状,并说明理由.
分析 (1)利用圆周角定理可得∠BAC=∠CPB,∠ABC=∠APC,而∠APC=∠CPB=60°,所以∠BAC=∠ABC=60°,从而可判断△ABC的形状;
(2)由(1)结论知AB=AC,推出△PCA≌△DBA,根据全等三角形的性质得到∠D=∠APC=60°,由于∠DPA=180°-∠APC-∠CPB=60°,求得∠DAP=60°,即可得到结论.
解答 解:△ABC是等边三角形.
证明如下:在⊙O中,
∵∠BAC与∠CPB是$\widehat{BC}$所对的圆周角,∠ABC与∠APC是$\widehat{AC}$所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
故答案为:等边三角形;
(2)足等边三角形,
理由:由(1)结论知AB=AC,
∵BD=CP,∠PCA=∠DBA,
在△PCA与△DBA中,$\left\{\begin{array}{l}{AB=AC}\\{∠PCA=∠DBA}\\{BD=CP}\end{array}\right.$,
∴△PCA≌△DBA,
∴∠D=∠APC=60°,
∵∠DPA=180°-∠APC=∠CPB=60°,
∴∠DAP=60°,
∴△ADP是等边三角形.
点评 本题考查了全等三角形的判定和性质,圆周角定理.同弧所对的圆周角相等,并且等于它所对的圆心角的一半.也考查了等边三角形的判定方法.

练习册系列答案
相关题目
15.下面四省电视台标示图案中,属于轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.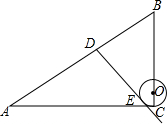 如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,点O为BC上的点,⊙O的半径OC=1,点D是AB边上的动点,过点D作⊙O的一条切线DE(点E为切点),则线段DE的最小值为( )
如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,点O为BC上的点,⊙O的半径OC=1,点D是AB边上的动点,过点D作⊙O的一条切线DE(点E为切点),则线段DE的最小值为( )
 如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,点O为BC上的点,⊙O的半径OC=1,点D是AB边上的动点,过点D作⊙O的一条切线DE(点E为切点),则线段DE的最小值为( )
如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,点O为BC上的点,⊙O的半径OC=1,点D是AB边上的动点,过点D作⊙O的一条切线DE(点E为切点),则线段DE的最小值为( )| A. | $3\sqrt{2}-1$ | B. | $\sqrt{15}-1$ | C. | $\sqrt{15}$ | D. | 4 |
10.下列命题的逆命题正确的是( )
| A. | 对顶角相等 | |
| B. | 三边相等的三角形是等边三角形 | |
| C. | 如果一个四边形是正方形,那么它的四条边相等 | |
| D. | 如果一个四边形是矩形,那么它的对角线相等 |
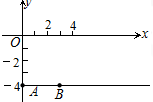 如图,已知A(0,-4)、B(3,-4),C为第四象限内一点且∠AOC=70°,若∠CAB=20°,则∠OCA=40°.
如图,已知A(0,-4)、B(3,-4),C为第四象限内一点且∠AOC=70°,若∠CAB=20°,则∠OCA=40°. 在Rt△ACB中,∠ACB=90°,CD⊥AB于点D,点E是线段BC上的动点,连AE交CD于点F.
在Rt△ACB中,∠ACB=90°,CD⊥AB于点D,点E是线段BC上的动点,连AE交CD于点F.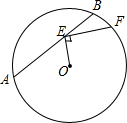 如图,已知⊙O的半径为5,弦AB=8,点E在AB上运动,连结OE,过点E作EF⊥OE交⊙O于点F,当EF最大时,OE+EF的值为7.
如图,已知⊙O的半径为5,弦AB=8,点E在AB上运动,连结OE,过点E作EF⊥OE交⊙O于点F,当EF最大时,OE+EF的值为7.