题目内容
19.已知正方形ABCD的边长为2cm,点P从点B开始以1cm/s的速度沿折线BC→CD→DA运动.△PAB的面积S(cm2)是点P运动时间t(s)的函数,若点P与点A或点B重合,则规定S=0(1)写出当0≤t≤2时,S关于t的函数关系式;
(2)当点P从点C运动到点D时,写出t的取值范围和S的值;
(3)写出点P从点D运动到点A时,S关于t的函数关系式,并写出t的取值范围.
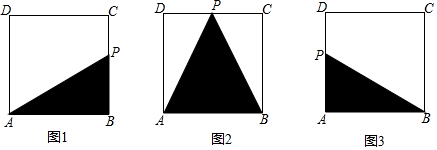
分析 (1)如图1,代入直角△ABP求S即可;
(2)如图2,根据速度求t的取值,代入面积公式求S;
(3)如图3,先表示AP=6-t,再求S.
解答 解:(1)如图1,当0≤t≤2时,P在BC边上运动,
由题意得:PB=t,AB=2,
∴S=$\frac{1}{2}$AB•PB=$\frac{1}{2}$×2t=t;
(2)∵BC=2,BC+CD=4,
∴当点P从点C运动到点D时,如图2,2≤t≤4,
∴S=$\frac{1}{2}$AB•BC=$\frac{1}{2}$×2×2=2;
(3)如图3,∵BC+CD=4,BC+CD+AD=6,
∴4≤t≤6,
由题意得:AP=6-t,
∴S=$\frac{1}{2}$AB•AP=$\frac{1}{2}$×2×(6-t)=6-t(4≤t≤6).
点评 本题考查了正方形的性质、三角形的面积以及动点运动问题,根据面积公式列式计算是本题的关键,注意利用数形观察三角形的形状,从而准确求三角形的面积.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
9.一元二次方程x(x-2)=2-x的根是( )
| A. | x=2 | B. | x1=0,x2=-2 | C. | x1=2,x2=-1 | D. | x=-1 |
10.若∠1和∠2互补,∠2与∠3互补,若∠1=68°,则∠3=( )
| A. | 28° | B. | 68° | C. | 118° | D. | 90° |
9. 如图是校园花圃一角,有的同学为了省时间图方便,在花圃中踩出了一条小道,这些同学这样做的数学道理是( )
如图是校园花圃一角,有的同学为了省时间图方便,在花圃中踩出了一条小道,这些同学这样做的数学道理是( )
 如图是校园花圃一角,有的同学为了省时间图方便,在花圃中踩出了一条小道,这些同学这样做的数学道理是( )
如图是校园花圃一角,有的同学为了省时间图方便,在花圃中踩出了一条小道,这些同学这样做的数学道理是( )| A. | 点动成线 | B. | 两点之间直线最短 | ||
| C. | 两点之间线段最短 | D. | 两点确定一条直线 |
 一个几何体由一些完全相同的小立方块搭成,从正面和从上面看到的这个几何体的形状如下,那么搭成这样一个几何体,最少需要6个这样的小立方块,最多需要8个这样的小立方块.
一个几何体由一些完全相同的小立方块搭成,从正面和从上面看到的这个几何体的形状如下,那么搭成这样一个几何体,最少需要6个这样的小立方块,最多需要8个这样的小立方块. 如图,已知△ABC.
如图,已知△ABC.