题目内容
已知二次函数y=x2+bx+c过点(0,-3)和(-1,2m-2)对于该二次函数有如下说法:
①它的图象与x轴有两个公共点;
②若存在一个正数x0,使得当x<x0时,函数值y随x的增大而减小,则m>0;若存在一个负数x0,使得当x>x0时,函数值y随x的增大而增大,则m<0;
③若将它的图象向左平移3个单位后过原点,则m=-1;
④若当x=2时的函数值与x=2012时的函数值相等,则当x=20时的函数值为-3.
其中正确的说法的个数是( )
①它的图象与x轴有两个公共点;
②若存在一个正数x0,使得当x<x0时,函数值y随x的增大而减小,则m>0;若存在一个负数x0,使得当x>x0时,函数值y随x的增大而增大,则m<0;
③若将它的图象向左平移3个单位后过原点,则m=-1;
④若当x=2时的函数值与x=2012时的函数值相等,则当x=20时的函数值为-3.
其中正确的说法的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:二次函数的性质
专题:
分析:把已知点的坐标代入可得y=x2-2mx-3,可利用方程x2-2mx-3=0的判别式判断①;可求得其对称轴为x=m,结合二次函数的增减性可判断②;根据左加右减的原则,可求得平移后的解析式,可判断③;根据二次函数的对称性,可求得对称轴,可求得m的值,再把x=20代入,可求得对应函数值,可判断④;可得出答案.
解答:解:
∵二次函数y=x2+bx+c过点(0,-3)和(-1,2m-2)
∴代入可求得c=-3,b=-2m,
∴二次函数解析式为y=x2-2mx-3,
令y=0可得x2-2mx-3=0,则其判别式△=4m2+12>0,故二次函数图象与x轴有两个公共点,
∴①正确;
∴二次函数的对称轴为x=m,且二次函数图象开口向上,
∴若存在一个正数x0,使得当x<x0时,函数值y随x的增大而减小,则m>0;若存在一个负数x0,使得当x>x0时,函数值y随x的增大而增大,则m<0,
∴②正确;
由平移可得向左平移3个单位后其函数解析式为y=(x+3)2-2m(x+3)-3,把点(0,0)代入可得m=1,
∴③不正确;
由当x=2时的函数值与x=2012时的函数值相等,代入可求得m=1007,
∴函数解析式为y=x2-2014x-3,
当x=20时,代入可得y=400-4028-3≠-3,
∴④不正确;
综上可知正确的有两个,
故选B.
∵二次函数y=x2+bx+c过点(0,-3)和(-1,2m-2)
∴代入可求得c=-3,b=-2m,
∴二次函数解析式为y=x2-2mx-3,
令y=0可得x2-2mx-3=0,则其判别式△=4m2+12>0,故二次函数图象与x轴有两个公共点,
∴①正确;
∴二次函数的对称轴为x=m,且二次函数图象开口向上,
∴若存在一个正数x0,使得当x<x0时,函数值y随x的增大而减小,则m>0;若存在一个负数x0,使得当x>x0时,函数值y随x的增大而增大,则m<0,
∴②正确;
由平移可得向左平移3个单位后其函数解析式为y=(x+3)2-2m(x+3)-3,把点(0,0)代入可得m=1,
∴③不正确;
由当x=2时的函数值与x=2012时的函数值相等,代入可求得m=1007,
∴函数解析式为y=x2-2014x-3,
当x=20时,代入可得y=400-4028-3≠-3,
∴④不正确;
综上可知正确的有两个,
故选B.
点评:本题主要考查二次函数的性质及与方程的关系,掌握二次函数的对称轴、增减性及图象的平移是解题的关键.注意与一元二次方程的关系.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
 如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,AE=AD.连接DE、AC交于F,连接BF.则有下列3个结论:
如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,AE=AD.连接DE、AC交于F,连接BF.则有下列3个结论:①∠DEC=60°;②△ACD≌△ACE;③△CDE为等边三角形;
其中正确的结论是( )
| A、①② | B、①③ | C、③ | D、①②③ |
计算:
+
=( )
| 1 |
| a |
| 1 |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
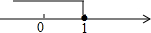 下列说法错误的是( )
下列说法错误的是( )| A、不等式x-3<-2的解集为x<1 |
| B、不等式x+2≤-2的最大负整数解为-1 |
| C、若不等式-3x+7<-2x成立,则不等式2x>9成立 |
| D、不等式-x≥-1的解集表示在数轴上如图所示 |
 如图,几块大小不等的正方形纸片无重叠地铺满了一块长方形.已知正方形纸片A的边长为7,求最小的正方形纸片的边长.
如图,几块大小不等的正方形纸片无重叠地铺满了一块长方形.已知正方形纸片A的边长为7,求最小的正方形纸片的边长.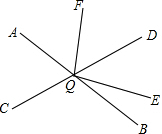 如图,直线AB,CD相交于点O,∠DOE:∠BOE=4:1,OF平分∠AOD,∠AOC=∠AOF-15°,求∠EOF的度数.
如图,直线AB,CD相交于点O,∠DOE:∠BOE=4:1,OF平分∠AOD,∠AOC=∠AOF-15°,求∠EOF的度数.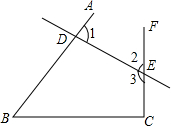 如图,
如图,