题目内容
3. 如图,l1∥l2,则α=( )
如图,l1∥l2,则α=( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
分析 首先过点B作BE∥l1,由l1∥l2,即可得BE∥l1∥l2,根据两直线平行,同旁内角互补与两直线平行,内错角相等,即可求得∠ABE与∠CBE度数,则可求得角α的度数.
解答  解:过点B作BE∥l1,
解:过点B作BE∥l1,
∵l1∥l2,
∴BE∥l1∥l2,
∴∠ABE+∠A=180°,∠CBE=∠C=30°,
∴∠ABE=180°-∠A=180°-140°=40°,
∴∠α=∠ABE+∠CBE=70°.
故选C.
点评 此题考查了平行线的性质.解题的关键是注意掌握两直线平行,同旁内角互补与两直线平行,内错角相等定理的应用,以及辅助线的作法.

练习册系列答案
相关题目
13.某商品的进价是80元,打8折售出后,仍可获利10%,你认为标在标签上的价格为( )
| A. | 110元 | B. | 120元 | C. | 150元 | D. | 160元 |
18.某公司有A、B两种型号的客车共15辆,它们的载客量,每天的租金和车辆数如下表所示,已知在15辆客车都坐满的情况下,共载客570人
(1)求表中a,b的值;
(2)某中学计划租用A、B两种型号的客车共5辆,同时送七年级师生到基地参加社会实践活动,已知该中学租车的总费用不超过1900元.
①求最多能租用多少辆A型号客车?
②若七年级的师生共有195人,请写出所有可能的租车方案,并确定最省钱的租车方案.
| A型号客车 | B型号客车 | |
| 载客量(人/辆) | 45 | 30 |
| 租金(元/辆) | 400 | 280 |
| 车辆数(辆) | a | b |
(2)某中学计划租用A、B两种型号的客车共5辆,同时送七年级师生到基地参加社会实践活动,已知该中学租车的总费用不超过1900元.
①求最多能租用多少辆A型号客车?
②若七年级的师生共有195人,请写出所有可能的租车方案,并确定最省钱的租车方案.
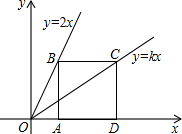 如图,已知四边形ABCD是正方形,点B,C分别在两条直线y=2x和y=kx上,点A,D是x轴上两点.
如图,已知四边形ABCD是正方形,点B,C分别在两条直线y=2x和y=kx上,点A,D是x轴上两点.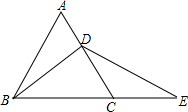 如图所示,△ABC为等边三角形,BD为中线,延长BC至E,使 DE=BD.
如图所示,△ABC为等边三角形,BD为中线,延长BC至E,使 DE=BD.