Question

15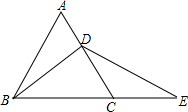．如图所示，△ABC为等边三角形，BD为中线，延长BC至E，使 DE=BD．
求证：（1）CE=$\frac{1}{2}$BC．
（2）把（1）中的BD为中线换成其它什么条件也能得到同样的结论．

Answer 1

分析 （1）根据已知条件，△ABC为等边三角形，BD为中线，可知∠DBE=30°，∠DCE=120°，∠CDE=30°，求得CD=CE即可解答．
（2）根据等腰三角形三线合一的性质解答即可．

解答 证明：（1）∵△ABC为等边三角形，BD为中线，
∴AD=CD=$\frac{1}{2}$AC=$\frac{1}{2}$BC，∠DBC=$\frac{1}{2}$∠ABC=$\frac{1}{2}$×60°=30°．
∵DE=BD，
∴∠DBC=∠DEC=30°．
又∵∠ACB=60°，是△DCE的一个外角，
∴∠EDC=∠ACB-∠DEC=60°-30°=30°．
∴CE=$\frac{1}{2}$BC．
（2）根据等腰三角形三线合一的性质：把（1）中的BD为中线换成BD是高或是∠ABC的角平分线也能得到同样的结论．

点评 本题考查了等边三角形的性质及全等三角形的判定与性质；巧妙利用三角形外角与内角的关系是解答本题的关键．