��Ŀ����
17����ͼ��������y=ax2+bx-5��x���ཻ��A��1��0����B��5��0������y���ཻ�ڵ�C���Գ�����x���ཻ�ڵ�M��P����������һ�����㣨��P��M��C����ͬһ��ֱ���ϣ����ֱ����A��B��AD��CP��BE��CP������ֱ�Ϊ��D��E������MD��ME��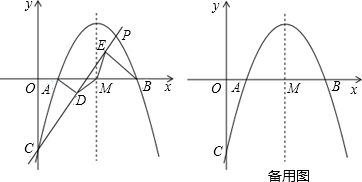
��1���������ߵĽ���ʽ��
��2������P�ڵ�һ�����ڣ�ʹS��PAB=S��PAC�����P�����ꣻ
��3����P���˶������У���MDE�ܷ�Ϊ����ֱ�������Σ����ܣ������ʱ��P�����ꣻ�����ܣ���˵�����ɣ�
���� ��1������A��B��������������ߵĽ���ʽ�������a=-1��b=6���Ӷ�����������ߵĽ���ʽ��
��2�����P������Ϊ��a��-a2+6a-5����Ȼ�����ֱ��CP�Ľ���ʽΪy=��6-a��x-5����y=0���Ӷ������ֱ��CP��x��Ľ������꣬������S��PAB=S��PAC�г�����a�ķ��̣��Ӷ������a=4��
��3������MED=90��ʱ����E��B��M��һ��ֱ���ϣ����������������ͬ������MDE=90��ʱ��������������DME=90��ʱ����ֱ��PC��Գ��ύ�ڵ�N������֤����ADM�ա�NEM���õ�MN=AM���Ӷ���õ�N����Ϊ��3��2����������õ�N����C���꣬���ֱ��PC�Ľ���ʽ���������ֱ��PC�������ߵĽ���ʽ�������P�����꣮
��� �⣺��1���߽���A��B���������ã�$\left\{\begin{array}{l}{a+b-5=0}\\{25a+5b-5=0}\end{array}\right.$����ã�a=-1��b=6��
�������ߵĽ���ʽΪy=-x2+6x-5��
��2����ͼ1��ʾ����PC��x��Ľ���ΪF��
����x=0����y=-5��
��C��0��-5����
��ֱ��PC�Ľ���ʽΪy=kx-5����P������Ϊ��a��-a2+6a-5����
����P���������PC�Ľ���ʽ�ã�ka=-a2+6a-5��
��ã�a=0����ȥ����k=6-a��
��ֱ��PC�Ľ���ʽΪy=��6-a��x-5��
��y=0���6-a��x-5=0��
��ã�x=$\frac{5}{6-a}$��
���F�����꣨$\frac{5}{6-a}$��0����
��S��PAB=S��PAC��
��$\frac{1}{2}$��$\frac{5}{6-a}$-1����-a2+6a-5+5��=$\frac{1}{2}��4$����-a2+6a-5����
��ã������ã�a2-5a+4=0��
��ã�a=1����ȥ����a=4��
��a=4ʱ��-a2+6a-5=-16+24-5=3��
���P��������4��3����
��3���������߽���ʽΪy=-x2+6x-5��
��Գ�����ֱ��x=3��
��M��3��0����
�ٵ���MED=90��ʱ����E��B��M��һ��ֱ���ϣ����������������
��ͬ��������MDE=90��ʱ����������
�۵���DME=90��ʱ����ͼ2��ʾ��
��ֱ��PC��Գ��ύ�ڵ�N��
��EM��DM��MN��AM��
���EMN=��DMA��
�ߡ�MDE=45�㣬��EDA=90�㣬
���MDA=135�㣮
�ߡ�MED=45�㣬
���NEM=135�㣮
���ADM=��NEM=135�㣮
�ڡ�ADM���NEM�У�$\left\{\begin{array}{l}{��EMN=��DMA}\\{EM=DM}\\{��ADM=��NEM=135��}\end{array}\right.$��
���ADM�ա�NEM��ASA����
��MN=MA��
��MN=MA=2��
��N��3��2����
��ֱ��PC����ʽΪy=kx+b������N��3��2����C��0��-5������ֱ�ߵĽ���ʽ�ã�$\left\{\begin{array}{l}{3k+b=2}\\{b=-5}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=\frac{7}{3}}\\{b=-5}\end{array}\right.$��
��ֱ��PC�Ľ���ʽΪy=$\frac{7}{3}$x-5��
��y=$\frac{7}{3}$x-5���������߽���ʽ�ã�$\frac{7}{3}$x-5=-x2+6x-5����ã�x=0��x=$\frac{11}{3}$��
��x=0ʱ������Ϊ��C����x=$\frac{11}{3}$ʱ��y=$\frac{7}{3}$x-5=$\frac{32}{9}$��
��P��$\frac{11}{3}$��$\frac{32}{9}$����
������������MDE�ܳ�Ϊ����ֱ�������Σ���ʱ��P����Ϊ��$\frac{11}{3}$��$\frac{32}{9}$����
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ������һ�κ����Ͷ��κ����Ľ���ʽ������ֱ�������ε����ʡ�ȫ�������ε����ʺ��ж���֤�á�ADM�ա�NEM��ASA�����Ӷ��õ���N�������ǽ���Ĺؼ���

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
 ��ͼ����֪������ƽ�е�����$\overrightarrow a��\overrightarrow b$���Ȼ�����������$��\frac{1}{2}\overrightarrow a+3\overrightarrow b��-��\frac{3}{2}\overrightarrow a+\overrightarrow b��$��
��ͼ����֪������ƽ�е�����$\overrightarrow a��\overrightarrow b$���Ȼ�����������$��\frac{1}{2}\overrightarrow a+3\overrightarrow b��-��\frac{3}{2}\overrightarrow a+\overrightarrow b��$�� ��������A��B���㣬A��B����࣬��֪��B��Ӧ����Ϊ2����A��Ӧ����Ϊa��
��������A��B���㣬A��B����࣬��֪��B��Ӧ����Ϊ2����A��Ӧ����Ϊa��