题目内容
19.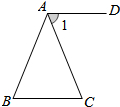 如图,在△ABC中,AB=AC,过A点作AD∥BC,若∠BAD=110°,则∠BAC的大小为( )
如图,在△ABC中,AB=AC,过A点作AD∥BC,若∠BAD=110°,则∠BAC的大小为( )| A. | 30° | B. | 40° | C. | 50° | D. | 70° |
分析 根据平行线的性质求出∠C,根据等腰三角形的性质得出∠B=∠C=70°,根据三角形内角和定理求出即可.
解答 解:∵AB=AC,
∴∠B=∠C,
∵AD∥BC,∠1=70°,
∴∠C=∠1=70°,
∴∠B=70°,
∴∠BAC=180°-∠B-∠C=180°-70°-70°=40°,
故选B.
点评 本题考查了三角形内角和定理,等腰三角形的性质,平行线的性质的应用,解此题的关键是求出∠C的度数和得出∠B=∠C,注意:三角形内角和等于180°,两直线平行,内错角相等.

练习册系列答案
相关题目
4.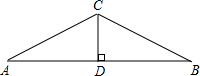 如图,要焊接一个等腰三角形钢架,钢架的底角为35°,高CD长为3米,则斜梁AC的长为( )米.
如图,要焊接一个等腰三角形钢架,钢架的底角为35°,高CD长为3米,则斜梁AC的长为( )米.
 如图,要焊接一个等腰三角形钢架,钢架的底角为35°,高CD长为3米,则斜梁AC的长为( )米.
如图,要焊接一个等腰三角形钢架,钢架的底角为35°,高CD长为3米,则斜梁AC的长为( )米.| A. | $\frac{3}{cos35°}$ | B. | $\frac{3}{tan35°}$ | C. | 3sin35° | D. | $\frac{3}{sin35°}$ |
9.下列运算不正确的是( )
| A. | a3•a2=a5 | B. | (x3)2=x9 | C. | x5+x5=2x5 | D. | (-ab)5÷(-ab)2=-a3b3 |
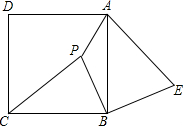 已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.
已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.