题目内容
7.若关于x的方程mx2-4x+2=0有实数根,则m的取值范围是m≤2.分析 分两种情况:m=0,方程为已知方程有一元一次方程,方程有实数根;当m≠0,则△≥0,由此建立关于m的不等式,然后解不等式即可求出m的取值范围.
解答 解:当m=0,方程为-4x+2=0一元一次方程,方程有实数根;
由题意知m≠0,
△=16-8m≥0,
∴m≤2.
综上所知:m≤2.
故答案为:m≤2.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的两个实数根;当△=0时,方程有两个相等的两个实数根;当△<0时,方程无实数根.

练习册系列答案
相关题目
2.已知x2+3x+5的值为11,则代数式3x2+9x-12的值为( )
| A. | 3 | B. | 6 | C. | 9 | D. | -9 |
19.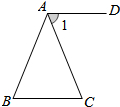 如图,在△ABC中,AB=AC,过A点作AD∥BC,若∠BAD=110°,则∠BAC的大小为( )
如图,在△ABC中,AB=AC,过A点作AD∥BC,若∠BAD=110°,则∠BAC的大小为( )
 如图,在△ABC中,AB=AC,过A点作AD∥BC,若∠BAD=110°,则∠BAC的大小为( )
如图,在△ABC中,AB=AC,过A点作AD∥BC,若∠BAD=110°,则∠BAC的大小为( )| A. | 30° | B. | 40° | C. | 50° | D. | 70° |
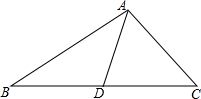 如图,AD是△ABC的中线,∠CAD=60°,AD=4,AB-AC=2,则BC的长为2$\sqrt{21}$.
如图,AD是△ABC的中线,∠CAD=60°,AD=4,AB-AC=2,则BC的长为2$\sqrt{21}$.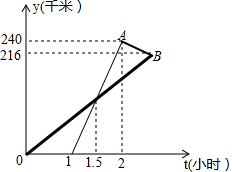 十一期间,小明和小亮相约从长春出发到某市某游乐园游玩,小明乘私家车从长春出发1小时后,小亮乘“和谐号”动车从长春出发,先到某市火车站A,然后乘出租车去游乐园B(换车时间忽略不计),两人恰好同时到达游乐园,他们离开长春的距离y(千米)与小明乘车时间t(时)的函数图象如图所示.
十一期间,小明和小亮相约从长春出发到某市某游乐园游玩,小明乘私家车从长春出发1小时后,小亮乘“和谐号”动车从长春出发,先到某市火车站A,然后乘出租车去游乐园B(换车时间忽略不计),两人恰好同时到达游乐园,他们离开长春的距离y(千米)与小明乘车时间t(时)的函数图象如图所示.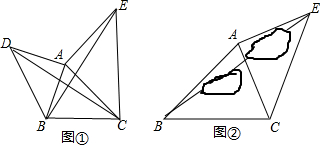
 甲乙两人玩纸牌游戏,如图是同一副扑克中的4张扑克牌的正面,将它们正面朝下后放在桌上,甲先从中抽出一张,乙从剩余的3张牌中也抽出一张.
甲乙两人玩纸牌游戏,如图是同一副扑克中的4张扑克牌的正面,将它们正面朝下后放在桌上,甲先从中抽出一张,乙从剩余的3张牌中也抽出一张.