题目内容
4.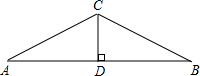 如图,要焊接一个等腰三角形钢架,钢架的底角为35°,高CD长为3米,则斜梁AC的长为( )米.
如图,要焊接一个等腰三角形钢架,钢架的底角为35°,高CD长为3米,则斜梁AC的长为( )米.| A. | $\frac{3}{cos35°}$ | B. | $\frac{3}{tan35°}$ | C. | 3sin35° | D. | $\frac{3}{sin35°}$ |
分析 利用锐角三角函数关系分别得出AC的长即可.
解答 解:因为等腰三角形钢架,钢架的底角为35°,高CD长为3米,
所以AC=$\frac{3}{sin35°}$,
故选D.
点评 此题主要考查了解直角三角形的应用,熟练应用锐角三角函数关系是解题关键.

练习册系列答案
相关题目
19.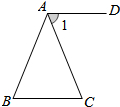 如图,在△ABC中,AB=AC,过A点作AD∥BC,若∠BAD=110°,则∠BAC的大小为( )
如图,在△ABC中,AB=AC,过A点作AD∥BC,若∠BAD=110°,则∠BAC的大小为( )
 如图,在△ABC中,AB=AC,过A点作AD∥BC,若∠BAD=110°,则∠BAC的大小为( )
如图,在△ABC中,AB=AC,过A点作AD∥BC,若∠BAD=110°,则∠BAC的大小为( )| A. | 30° | B. | 40° | C. | 50° | D. | 70° |
13.要使函数y=$\sqrt{x-1}$有意义,自变量x的取值范围是( )
| A. | x≥1 | B. | x≤1 | C. | x>1 | D. | x<1 |