题目内容
16. 如图,在正方形ABCD中,E是BC边的中点,把△ABE沿直线AE折叠,点B的对应点为B′,AB′的延长线交DC于点F,若FC=2,则正方形的边长为8.
如图,在正方形ABCD中,E是BC边的中点,把△ABE沿直线AE折叠,点B的对应点为B′,AB′的延长线交DC于点F,若FC=2,则正方形的边长为8.
分析 认真审题,连接EF,可以证明△EB′F≌△ECF,进而可以证明△ABE∽△ECF,得出两个三角形的边之间的比例关系,据此即可得出本题的答案.
解答 解:如图,连接EF,
∵四边形ABCD是正方形,
∴AB=BC,∠B=∠C=90°,
∵把△ABE沿直线AE折叠,点B的对应点为B′,E为BC的中点,
∴BE=EC=BB′,∠B=∠AB′E=∠EB′F=90°,∠AEB=∠AEB′
在Rt△EB′F和Rt△ECF中,
$\left\{\begin{array}{l}{EB′=EC}\\{EF=EF}\end{array}\right.$,
∴在Rt△EB′F≌Rt△ECF中,
∴∠B′EF=∠CEF,
∴∠AEB+∠CEF=90°,
∵∠BAE+∠AEB=90°,
∴∠BAE=∠CEF,
∴△ABE∽△ECF,
∴$\frac{FC}{BE}=\frac{EC}{AB}$,
即:$\frac{2}{BE}=\frac{1}{2}$,
解得:BE=4,
∴BC=8.
点评 本题主要考查了正方形的性质,以及翻折变换时,对应的线段相等,对应的角相等,还考查了相似三角形的判定与性质,有一定的难度,注意认真总结.

练习册系列答案
相关题目
8. 如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,则∠BAD的大小是( )
如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,则∠BAD的大小是( )
 如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,则∠BAD的大小是( )
如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,则∠BAD的大小是( )| A. | 45° | B. | 54° | C. | 40° | D. | 50° |
5.一木工将一根长100厘米的木条锯成30厘米与70厘米,要另找一跟木条,钉成一个三角形木架,应选择下列哪一根( )
| A. | 30厘米 | B. | 70厘米 | C. | 100厘米 | D. | 110厘米 |
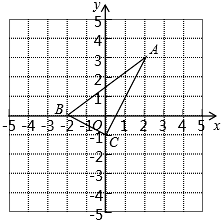 如图,直角坐标系中的网格由单位正方形构成,在格点△ABC中,点A的坐标为(2,3)
如图,直角坐标系中的网格由单位正方形构成,在格点△ABC中,点A的坐标为(2,3)
 如图,在三角形纸片ABC中,∠ACB=90°,BC=5,AB=13,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,点A与BC延长线上的点D重合,求CE的长.
如图,在三角形纸片ABC中,∠ACB=90°,BC=5,AB=13,在AC上取一点E,以BE为折痕,使AB的一部分与BC重合,点A与BC延长线上的点D重合,求CE的长. 如图,平面直角坐标系中,矩形ABCD的顶点A的坐标(3,6),AB=6,AD=3,将矩形向下平移m个单位,使矩形的两个顶点恰好同时落在某个反比例函数的图象上,则m=$\frac{3}{2}$或$\frac{15}{2}$.
如图,平面直角坐标系中,矩形ABCD的顶点A的坐标(3,6),AB=6,AD=3,将矩形向下平移m个单位,使矩形的两个顶点恰好同时落在某个反比例函数的图象上,则m=$\frac{3}{2}$或$\frac{15}{2}$. 如图,已知AB∥CD,点P在直线CD上,∠APB=100°,∠A=(2x+12)°,∠BPD=(4x+8)°,那么x=10.
如图,已知AB∥CD,点P在直线CD上,∠APB=100°,∠A=(2x+12)°,∠BPD=(4x+8)°,那么x=10.