题目内容
8.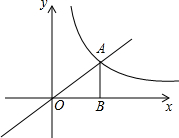 如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx的图象交于点A,AB垂直于x轴,垂足为B,并且AB=OB=2.
如图,反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx的图象交于点A,AB垂直于x轴,垂足为B,并且AB=OB=2.(1)求k和m的值;
(2)将△ABO绕O点逆时针旋转90°,得到△A′B′O,请画出旋转后的图形,并写出点A′的坐标;
(3)过点A′作直线OA的平行线,交y轴与点C,连接AC,判定四边形AOA′C的形状,并说明理由.
分析 (1)由题意得出点A的坐标,把点A的坐标分别代入反比例函数和一次函数解析式,即可求出k和m的值;
(2)容易画出△ABO绕O点逆时针旋转90°后的图形;由旋转的性质得出∠OB′A′=∠OBA=90°,A′B′=AB=2,OB′=OB=2,∠A′OB′=∠AOB=45°,OA′=OA,即可得出点A′的坐标;
(3)由题意得出△AOB是等腰直角三角形,得出∠AOB=45°,∠A′OB′=∠AOB=45°,证出A′C=AO,得出四边形AOA'C是平行四边形,再由∠A′OA′=90°,OA=OA′,即可得出四边形AOA′C是正方形.
解答 解:(1)∵AB⊥x轴,垂足为B,并且AB=OB=2,
∴点A的坐标为(2,2),
∵反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx的图象交于点A,
∴2=$\frac{k}{2}$,2=2m
∴k=4,m=1.
(2)将△ABO绕O点逆时针旋转90°,得到△A′B′O,所画图形如图1所示:
则∠OB′A′=∠OBA=90°,A′B′=AB=2,OB′=OB=2, ∠A′OB′=∠AOB=45°,OA′=OA,
∠A′OB′=∠AOB=45°,OA′=OA,
∴点A′的坐标为(-2,2);
(3)四边形AOA'C是正方形.理由如下:
如图2所示:
∵AB⊥x轴,垂足为B,并且AB=OB,
∴△AOB是等腰直角三角形.
∴∠AOB=45°,
∴∠A′OB′=∠AOB=45°,
∴∠A′OA′=∠COB=90°,
∵A′C∥OA,
∴∠A′CO=∠AOC=45°,
∴∠A′CO=∠A′OC,
∴A′C=A′O,
∴A′C=AO,
∴四边形AOA'C是平行四边形,
∵∠A′OA′=90°,
∴四边形AOA′C是矩形,
又∵OA=OA′,
∴四边形AOA′C是正方形.
点评 本题是反比例函数综合题目,考查了反比例函数和一次函数解析式的求法、等腰直角三角形的判定与性质、坐标与图形性质、平行四边形的判定以及矩形、菱形、正方形的判定等知识;本题综合性强,有一定难度.

| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | (a+3)(a-3)=a2-9 | B. | x2+x-5=x(x-1)-5 | C. | a2+a=a(a+1) | D. | x3 y=x•x2•y |




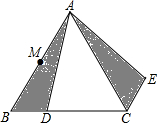 如图,△ABC是等边三角形,D是BC上一点,△ABD经过逆时针旋转后到达△ACE的位置.
如图,△ABC是等边三角形,D是BC上一点,△ABD经过逆时针旋转后到达△ACE的位置.