题目内容
7. 张师傅根据某几何体零件,按1:1的比例画出准确的三视图(都是长方形)如图,已知EF=4cm,FG=12cm,AD=10cm.
张师傅根据某几何体零件,按1:1的比例画出准确的三视图(都是长方形)如图,已知EF=4cm,FG=12cm,AD=10cm.(1)说出这个几何体的名称;
(2)求这个几何体的表面积S;
(3)求这个几何体的体积V.
分析 (1)由主视图、左视图、俯视图都是长方形,可知这个几何体是长方体;
(2)由图可知,长方体的长为12cm,宽为4cm,高为10cm,根据长方体的表面积公式列式计算即可;
(3)根据长方体的体积=长×宽×高列式计算即可.
解答 解:(1)由于主视图和左视图为长方形可得此几何体为柱体,由俯视图为长方形可得这个几何体是长方体;
(2)由图可知,长方体的长为12cm,宽为4cm,高为10cm,
则这个长方体的表面积S=2(12×4+12×10+4×10)=416(cm2);
(3)这个几何体的体积V=12×4×10=480(cm3).
点评 本题考查了由三视图判断几何体,由三视图想象几何体的形状,首先,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.由物体的三视图想象几何体的形状是有一定难度的,可以从以下途径进行分析:
①根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,以及几何体的长、宽、高;
②从实线和虚线想象几何体看得见部分和看不见部分的轮廓线;
③熟记一些简单的几何体的三视图对复杂几何体的想象会有帮助;
④利用由三视图画几何体与有几何体画三视图的互逆过程,反复练习,不断总结方法.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
17.关于反比例函数y=$\frac{2}{x}$,下列说法正确的是( )
| A. | 函数图象位于二、四象限 | B. | 经过点(-4,0.5) | ||
| C. | y的值随x的增大而增大 | D. | 函数图象关于直线y=x轴对称 |
2. 如图,顺次连结圆内接矩形各边的中点,得到菱形ABCD,若BD=8,BE=5,则菱形ABCD的边长为( )
如图,顺次连结圆内接矩形各边的中点,得到菱形ABCD,若BD=8,BE=5,则菱形ABCD的边长为( )
 如图,顺次连结圆内接矩形各边的中点,得到菱形ABCD,若BD=8,BE=5,则菱形ABCD的边长为( )
如图,顺次连结圆内接矩形各边的中点,得到菱形ABCD,若BD=8,BE=5,则菱形ABCD的边长为( )| A. | 6 | B. | $\sqrt{41}$ | C. | 9 | D. | $\sqrt{89}$ |
12.下列不是一元一次方程的是( )
| A. | 5y+3=3y+7 | B. | 1+2y=3 | C. | $\frac{2y}{3}+\frac{5}{y}=3$ | D. | y=-7 |
19.如果有理数a,b的倒数的绝对值分别是3和2,那么a+b的值是( )
| A. | $\frac{5}{6}$ | B. | -$\frac{5}{6}$ | C. | $±\frac{5}{6}$ | D. | 有4个不同的值 |
16. 一次函数y=kx=b(b≠0)的图象如图所示,当y>0时,x的取值范围是( )
一次函数y=kx=b(b≠0)的图象如图所示,当y>0时,x的取值范围是( )
 一次函数y=kx=b(b≠0)的图象如图所示,当y>0时,x的取值范围是( )
一次函数y=kx=b(b≠0)的图象如图所示,当y>0时,x的取值范围是( )| A. | x>2 | B. | x>0 | C. | x<2 | D. | x<0 |
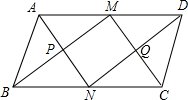 如图,M、N分别是平行四边形ABCD的对边AD、BC的中点,且AD=2AB,连接AN、DN、BM、CM,交点分别为P、Q.请判断四边形PMQN是什么特殊四边形?并证明你的结论.
如图,M、N分别是平行四边形ABCD的对边AD、BC的中点,且AD=2AB,连接AN、DN、BM、CM,交点分别为P、Q.请判断四边形PMQN是什么特殊四边形?并证明你的结论. 如图,在等腰梯形ABCD中,AD∥BC,过点A作AE∥CD,交BC于点E,若AB=2,AD=1.则四边形AECD的周长是6.
如图,在等腰梯形ABCD中,AD∥BC,过点A作AE∥CD,交BC于点E,若AB=2,AD=1.则四边形AECD的周长是6.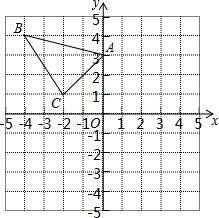 △ABC在直角坐标系内如所示.
△ABC在直角坐标系内如所示.