题目内容
对于形如x2+2xa+a2这样的二次三项式,可以用公式法将它分解成(x+a)2的形式.但对于二次三项式x2+2xa-3a2,就不能直接运用公式了.此时,我们可以在二次三项式x2+2xa-3a2中先加上一项a2,使它与x2+2xa的和成为一个完全平方式,再减去a2,整个式子的值不变,于是有:
x2+2xa-3a2=(x2+2xa+a2)-a2-3a2
=(x+a)2-4a2
=(x+a)2-(2a)2
=(x+3a)(x-a)
像这样,先添一适当项,使式中出现完全平方式,再减去这个项,使整个式子的值不变的方法称为“配方法”,利用“配方法”,解决下列问题:
(1)分解因式:a2-6a+8;
(2)若x2-2xy+2y2-2y+1=0,求xy的值.
x2+2xa-3a2=(x2+2xa+a2)-a2-3a2
=(x+a)2-4a2
=(x+a)2-(2a)2
=(x+3a)(x-a)
像这样,先添一适当项,使式中出现完全平方式,再减去这个项,使整个式子的值不变的方法称为“配方法”,利用“配方法”,解决下列问题:
(1)分解因式:a2-6a+8;
(2)若x2-2xy+2y2-2y+1=0,求xy的值.
考点:因式分解的应用,完全平方式
专题:阅读型
分析:(1)前两项加9再减9,可以组成完全平方式;
(2)分组利用完全平方公式因式分解,进一步利用非负数的性质求得x、y,代入求得答案即可.
(2)分组利用完全平方公式因式分解,进一步利用非负数的性质求得x、y,代入求得答案即可.
解答:解:(1)a2-6a+8
=a2-6a+9-9+8
=(a-3)2-1
=(a-2)(a-4).
(2)∵x2-2xy+2y2-2y+1=0,
∴x2-2xy+y2+y2-2y+1=0,
(x-y)2+(y-1)2=0,
∵(x-y)2,≥0,(y-1)2≥0,
∴x-y=0,y-1=0,
x=y=1,
∴xy=1.
=a2-6a+9-9+8
=(a-3)2-1
=(a-2)(a-4).
(2)∵x2-2xy+2y2-2y+1=0,
∴x2-2xy+y2+y2-2y+1=0,
(x-y)2+(y-1)2=0,
∵(x-y)2,≥0,(y-1)2≥0,
∴x-y=0,y-1=0,
x=y=1,
∴xy=1.
点评:本题考查利用完全平方公式分解因式,配方法是数学习题里经常出现的方法,应熟练掌握.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
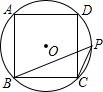 如图,正方形ABCD是⊙O的内接正方形,点P是劣弧BC上不同于点B的任意一点,则∠BPA的度数是( )
如图,正方形ABCD是⊙O的内接正方形,点P是劣弧BC上不同于点B的任意一点,则∠BPA的度数是( )| A、45° | B、60° |
| C、75° | D、90° |
 如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,BD=EC.
如图,已知△ABC是等边三角形,D为边AC的中点,AE⊥EC,BD=EC.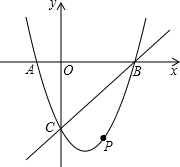 如图,抛物线经过A(-1,0),B(5,0),C(0,-
如图,抛物线经过A(-1,0),B(5,0),C(0,-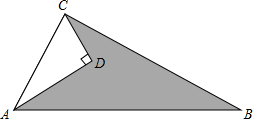 已知:如图,AD=4,CD=3,∠ADC=90°,AB=13,∠ACB=90°,求图形中阴影部分的面积.
已知:如图,AD=4,CD=3,∠ADC=90°,AB=13,∠ACB=90°,求图形中阴影部分的面积.