题目内容
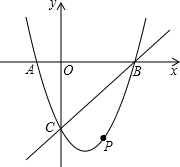 如图,抛物线经过A(-1,0),B(5,0),C(0,-
如图,抛物线经过A(-1,0),B(5,0),C(0,-| 5 |
| 2 |
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点M,使MA+MC的值最小,求点M的坐标;
(3)当点P运动到什么位置时,△PBC的面积最大,并求出此时P点的坐标和△PBC的最大面积.
考点:二次函数综合题
专题:
分析:(1)A(-1,0),B(5,0),C(0,-
)代入y=ax2+bx+c,即可得出抛物线的解析式,
(2)点B是点A关于抛物线对称轴的对称点,在抛物线的对称轴上有一点M,要使MA+MC的值最小,则点M就是BC与抛物线对称轴的交点,把B(5,0),C(0,-
)代入y=kx+b,求出直线BC的解析式,把抛物线对称轴x=2代入即可得到点M的坐标,
(3)过点P作l∥BC,交y轴于Q点,当l与抛物线只有唯一的公共点P时,△PBC的面积最大,联立方程利用△可求出设此时l的解析式,可求出点P的作坐标,作CN⊥l,利用
=
求出CN,即可得出△PBC的面积.
| 5 |
| 2 |
(2)点B是点A关于抛物线对称轴的对称点,在抛物线的对称轴上有一点M,要使MA+MC的值最小,则点M就是BC与抛物线对称轴的交点,把B(5,0),C(0,-
| 5 |
| 2 |
(3)过点P作l∥BC,交y轴于Q点,当l与抛物线只有唯一的公共点P时,△PBC的面积最大,联立方程利用△可求出设此时l的解析式,可求出点P的作坐标,作CN⊥l,利用
| CN |
| CQ |
| OB |
| BC |
解答:解:(1)设抛物线的解析式为y=ax2+bx+c,把A(-1,0),B(5,0),C(0,-
)代入解析式,
得
,解得
,
所以抛物线的解析式为y=
x2-2x-
.
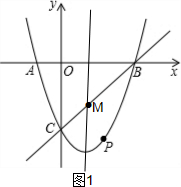
(2)如图1,点B是点A关于抛物线对称轴的对称点,在抛物线的对称轴上有一点M,要使MA+MC的值最小,
则点M就是BC与抛物线对称轴的交点,
∵抛物线的解析式为y=
x2-2x-
.
∴抛物线对称轴x=2,
设直线BC的解析式为y=kx+b,
把B(5,0),C(0,-
)代入得
,解得
.
∴直线BC的解析式为y=
x-
,
∵M的横坐标为2,
∴点M的坐标为(2,-
),
(3)过点P作l∥BC,交y轴于Q点,如图2,
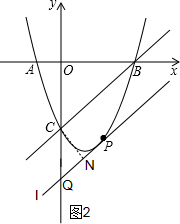
∵当l与抛物线只有唯一的公共点P时,△PBC的面积最大,设此时l的解析式为y=
x+n,
∴方程有唯一一组解,即
x2-2x-
=
x+n有相等的实数解,
整理得x2-5x-5-2n=0,△=52-4(-5-2n)=0,解得n=-
,y=
x-
,
∴此时P点坐标为(
,-
),
∵Q点坐标为(0,-
),
作CN⊥l,CQ=OQ-OC=
-
=
,
∵
=
=
=
,
∴CN=
•
=
,
∴△PBC的面积=
BC•CN=
×
×
=
.
| 5 |
| 2 |
得
|
|
所以抛物线的解析式为y=
| 1 |
| 2 |
| 5 |
| 2 |
(2)如图1,点B是点A关于抛物线对称轴的对称点,在抛物线的对称轴上有一点M,要使MA+MC的值最小,
则点M就是BC与抛物线对称轴的交点,

∵抛物线的解析式为y=
| 1 |
| 2 |
| 5 |
| 2 |
∴抛物线对称轴x=2,
设直线BC的解析式为y=kx+b,
把B(5,0),C(0,-
| 5 |
| 2 |
|
|
∴直线BC的解析式为y=
| 1 |
| 2 |
| 5 |
| 2 |
∵M的横坐标为2,
∴点M的坐标为(2,-
| 3 |
| 2 |
(3)过点P作l∥BC,交y轴于Q点,如图2,

∵当l与抛物线只有唯一的公共点P时,△PBC的面积最大,设此时l的解析式为y=
| 1 |
| 2 |
∴方程有唯一一组解,即
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
整理得x2-5x-5-2n=0,△=52-4(-5-2n)=0,解得n=-
| 45 |
| 8 |
| 1 |
| 2 |
| 45 |
| 8 |
∴此时P点坐标为(
| 5 |
| 2 |
| 35 |
| 8 |
∵Q点坐标为(0,-
| 45 |
| 8 |
作CN⊥l,CQ=OQ-OC=
| 45 |
| 8 |
| 5 |
| 2 |
| 25 |
| 8 |
∵
| CN |
| CQ |
| OB |
| BC |
| 5 | ||||
|
2
| ||
| 5 |
∴CN=
2
| ||
| 5 |
| 25 |
| 8 |
5
| ||
| 4 |
∴△PBC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
5
| ||
| 2 |
5
| ||
| 4 |
| 125 |
| 16 |
点评:本题主要考查了二次函数与方程、几何知识的综合应用,解题的关键是将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
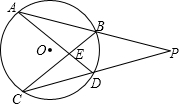 如图,AB、CD是⊙O的两条弦,延长AB、CD交于点P,连接AD、BC交于点E.∠P=30°,∠ABC=50°,则∠AEC为( )
如图,AB、CD是⊙O的两条弦,延长AB、CD交于点P,连接AD、BC交于点E.∠P=30°,∠ABC=50°,则∠AEC为( )| A、60° | B、65° |
| C、70° | D、80° |
已知下列命题:①抛物线y=3x2+5x-1与两坐标轴交点的个数为2个;②相等的圆心角所对的弦相等;③任何正多边形都有且只有一个外接圆;④三角形的外心到三角形各顶点的距离相等;⑤圆内接四边形对角相等;真命题的个数有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
下列方程中,一元二次方程的个数为( )
(1)2x2-3=0;(2)x2+y2=5;(3)
=5;(4)x2+
=2.
(1)2x2-3=0;(2)x2+y2=5;(3)
| x2-4 |
| 1 |
| x2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
已知圆锥的侧面积为12π,那么圆锥的母线l关于底面半径r的函数关系式是( )
| A、l=12r | ||
B、l=
| ||
| C、l=12-r | ||
D、l=
|
 如图,在△ABC中,∠C=90°,∠BAC=30°,AD=AB,求tan∠D=
如图,在△ABC中,∠C=90°,∠BAC=30°,AD=AB,求tan∠D=