Question

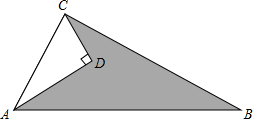已知：如图，AD=4，CD=3，∠ADC=90°，AB=13，∠ACB=90°，求图形中阴影部分的面积．

Answer 1

考点：勾股定理,勾股定理的逆定理

专题：

分析：根据勾股定理求出AC的长，再根据勾股定理求出BC的长，求出△ABC的面积，再求出△ACD的面积，相减即可．

解答：解：在Rt△ACD中，AC=

32+42

=5；
在Rt△ACD中，BC=

132-52

=12；
∴S_△ABC=

1

2

×5×12=30，
S_△ACD=

1

2

×4×3=6，
∴阴影部分面积为30-6=24．

点评：本题考查了勾股定理、三角形的面积，要灵活转化图形进行解答．