题目内容
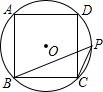如图，正方形ABCD是⊙O的内接正方形，点P是劣弧BC上不同于点B的任意一点，则∠BPA的度数是（ ）| A、45° | B、60° |
| C、75° | D、90° |
考点：圆周角定理
专题：
分析：首先连接OB，OC，由正方形ABCD是⊙O的内接正方形，可得∠BOC=90°，然后由圆周角定理，求得∠BPA的度数．
解答：
解：连接OB，OC，
∵正方形ABCD是⊙O的内接正方形，
∴∠BOC=90°，
∴∠BPA=
∠BOC=45°．
故选A．
解：连接OB，OC，∵正方形ABCD是⊙O的内接正方形，
∴∠BOC=90°，
∴∠BPA=
| 1 |
| 2 |
故选A．
点评：此题考查了圆周角定理以及圆内接正方形的性质．此题难度不大，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
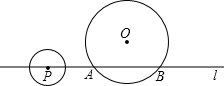如图，⊙O的半径为4cm，直线l与⊙O相交于A、B两点，AB=4| 3 |
| A、2cm＜d＜3cm或d＞5cm | ||
| B、2cm＜d＜4cm或d＞6cm | ||
| C、3cm＜d＜6cm | ||
D、2cm＜d＜4
|
下列方程中，一元二次方程的个数为（ ）
（1）2x2-3=0；（2）x2+y2=5；（3）
=5；（4）x2+
=2．
（1）2x2-3=0；（2）x2+y2=5；（3）
| x2-4 |
| 1 |
| x2 |
| A、1个 | B、2个 | C、3个 | D、4个 |