题目内容
13.随着“新年”临近,儿童礼品开始热销,某厂每月固定生产甲、乙两种礼品共100万件,甲礼品每件成本15元,乙礼品每件成本12元,现甲礼品每件售价22元,乙礼品每件售价18元,且都能全部售出.(1)若某月甲礼品的产量为x万件,总利润为y万元,写出y关于x的函数关系式.
(2)如果每月投入的总成本不超过1380万元,应怎样安排甲、乙礼品的产量,可使所获得的利润最大?
分析 (1)设生产甲礼品x万件,乙礼品(100-x)万件,根据收入=售价×产量列出函数关系式即可;
(2)设生产甲礼品x万件,乙礼品(100-x)万件,所获得的利润为y万元,根据成本不超过1380万元求出x的取值范围,然后根据利润=(售价-成本)×销量,列出函数关系式,求y的最大值;
解答 解:(1)设生产甲礼品x万件,乙礼品(100-x)万件,
由题意得:y=(22-15)x+(18-12)(100-x)=x+600;
(2)设生产甲礼品x万件,乙礼品(100-x)万件,所获得的利润为y万元,
由题意得:15x+12(100-x)≤1380,
∴x≤60,
利润y=(22-15)x+(18-12)(100-x)=x+600,
∵y随x增大而增大,
∴当x=60万件时,y有最大值660万元.
这时应生产甲礼品60万件,乙礼品40万件.
点评 本题考查了一次函数的应用,难度一般,解答本题的关键是读懂题意列出函数关系式并熟练掌握及一次函数最大值的方法.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
18.某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表.
(1)若工厂生产成本不多于35万元,且获利多于15万元,问工厂有哪几种生产方案?
(2)在(1)的条件下,哪种生产方案获利最大?并求出最大利润.
| A种产品 | B种产品 | |
| 成本(万元/件) | 2 | 5 |
| 利润(万元/件) | 1 | 3 |
(2)在(1)的条件下,哪种生产方案获利最大?并求出最大利润.
5.某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午8:00~12:00,下午14:00~18:00,每月25天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于45件.
生产产品件数与所用时间之间的关系见下表:
信息三:按件计酬,每生产一件甲产品可得6元,每生产一件乙产品可得10元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分?
(2)小王该月最多能得多少元?此时生产甲、乙两种产品分别多少件?
信息一:工作时间:每天上午8:00~12:00,下午14:00~18:00,每月25天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于45件.
生产产品件数与所用时间之间的关系见下表:
| 生产甲产品件数(件) | 生产乙产品件数(件) | 所用总时间(分) |
| 10 | 10 | 500 |
| 15 | 20 | 900 |
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分?
(2)小王该月最多能得多少元?此时生产甲、乙两种产品分别多少件?
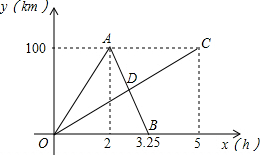 甲、乙两人分别从相距100km两地同时出发,相向而行.甲、乙两人距各自出发点的距离y(千米)与时间x(小时)之间的函数图象如图所示,其中折线OAB表示甲,线段OC表示乙.根据图象所提供的信息解答下列问题:
甲、乙两人分别从相距100km两地同时出发,相向而行.甲、乙两人距各自出发点的距离y(千米)与时间x(小时)之间的函数图象如图所示,其中折线OAB表示甲,线段OC表示乙.根据图象所提供的信息解答下列问题: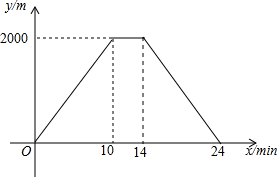 小明骑自行车从甲地到乙地,到达乙地后,休息了一段时间,然后原路返回,停在甲地.整个过程保持匀速前进,设小明出发x(min)后,到达距离甲地y(m)的地方,图中的折线表示的是y与x之间的函数关系.
小明骑自行车从甲地到乙地,到达乙地后,休息了一段时间,然后原路返回,停在甲地.整个过程保持匀速前进,设小明出发x(min)后,到达距离甲地y(m)的地方,图中的折线表示的是y与x之间的函数关系. 如图,在△ABC中,M、E把AC边三等分,MN∥EF∥BC,MN、EF把△ABC分成三部分,则自上而下三部分的面积比为1:3:5.
如图,在△ABC中,M、E把AC边三等分,MN∥EF∥BC,MN、EF把△ABC分成三部分,则自上而下三部分的面积比为1:3:5. 如图,点O、B的坐标分别为(0,0)、(3,0),将△OAB绕点O按逆时针方向旋转90°△OA′B′.
如图,点O、B的坐标分别为(0,0)、(3,0),将△OAB绕点O按逆时针方向旋转90°△OA′B′.