题目内容
12.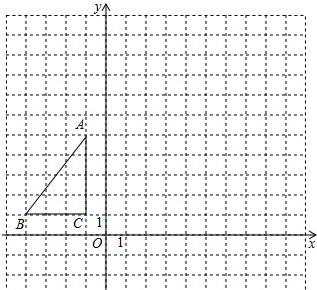 如图,在平面直角坐标系内,△ABC的顶点坐标分别为A(-1,5),B(-4,1),C(-1,1),将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′.
如图,在平面直角坐标系内,△ABC的顶点坐标分别为A(-1,5),B(-4,1),C(-1,1),将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′.(1)画出△AB′C′;
(2)写出点A,B关于原点O的对称点A″,B″的坐标;
(3)求出在△ABC旋转的过程中,点C经过的路径长.
分析 (1)利用网格特点和旋转的性质画出点B、C的对应点B′、C′即可得到,△AB′C′;
(2)根据关于原点对称的点的坐标特征求解;
(3)利用弧长公式计算.
解答 解:(1)如图,△AB′C′为所作;
(2)点A″的坐标为(1,-5);
点B″的坐标为(4,-1);
(3)点C经过的路径=$\frac{90•π•4}{180}$=2π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了弧长的计算.

练习册系列答案
相关题目
19.计算(-2)2007+3×(-2)2006的值为( )
| A. | -22006 | B. | 22006 | C. | (-2)2007 | D. | 22007 |
3.下列调查中,适合用全面调查的是( )
| A. | 调查某条河的河水受污染情况 | B. | 调查一批灯泡的使用寿命 | ||
| C. | 调查某班学生的视力情况 | D. | 调查我国中学生上网情况 |
7.若m是任意实数,则点A(m,3-m)一定不在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.下列图形中,是轴对称图形的为( )
| A. |  | B. |  | C. |  | D. |  |
 如图,AD∥BE∥CF,直线m,n与这三条平行线分别交于点A、B、C和点D、E、F,已知AB=5,BC=10,DE=4,则EF的长为( )
如图,AD∥BE∥CF,直线m,n与这三条平行线分别交于点A、B、C和点D、E、F,已知AB=5,BC=10,DE=4,则EF的长为( )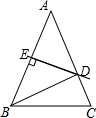 如图,△ABC中,AB=AC,AB的垂直平分线DE分别交AC、AB于点D、E.
如图,△ABC中,AB=AC,AB的垂直平分线DE分别交AC、AB于点D、E.