题目内容
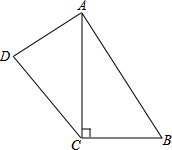已知：四边形ABCD中，AC⊥BC，AB=17，BC=8，CD=12，DA=9．（1）求AC的长；
（2）求四边形ABCD的面积．
考点：勾股定理的逆定理,勾股定理
专题：
分析：（1）根据勾股定理可求AC的长；
（2）先根据勾股定理的逆定理可求∠D=90°，再根据S四边形ABCD=S△ABC+S△ACD列式计算即可求解．
（2）先根据勾股定理的逆定理可求∠D=90°，再根据S四边形ABCD=S△ABC+S△ACD列式计算即可求解．
解答：解：（1）∵∠ACB=90°，
∴AC2=AB2-BC2=172-82=225，
∴AC=15；
（2）∵AD2+CD2=92+122=225=AC2，
∴∠D=90°，
∴S四边形ABCD=S△ABC+S△ACD=8×15÷2+12×9÷2=114．
∴AC2=AB2-BC2=172-82=225，
∴AC=15；
（2）∵AD2+CD2=92+122=225=AC2，
∴∠D=90°，
∴S四边形ABCD=S△ABC+S△ACD=8×15÷2+12×9÷2=114．
点评：本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
下列各数：0.51525354…，
，0，2，
，
，
，
，
中，无理数的个数是（ ）
|
| 7 |
| 3 | 27 |
| 1 |
| 27 |
| 1 |
| π |
| 3 | 9 |
| A、2个 | B、3个 | C、4个 | D、5个 |
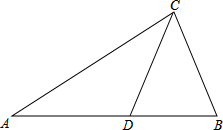下列是胡老师带领学生，探究SSA是否能判定两个三角形全等的过程，填空．
