题目内容
2.观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256…,则169的个位数字是( )| A. | 2 | B. | 4 | C. | 8 | D. | 6 |
分析 先根据题意得出2的n次幂的个位数字是以2,4,8,6四个数字为一个循环周期,再根据幂的乘方的性质将169转化为236,进而求解即可.
解答 解:∵21=2,22=4,23=8,24=16,
25=32,26=64,27=128,28=256…,
∴2的n次幂的个位数字是以2,4,8,6四个数字为一个循环周期,
∵169=(24)9=236,
36÷4=9,
∴169的个位数字与24的个位数字相同,为6.
故选D.
点评 本题考查了尾数特征,幂的乘方的性质,得到底数为2的幂的个位数字的循环规律是解决本题的关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
12.在-6,-3.5,0,2各数中,最小的数是( )
| A. | 2 | B. | -3.5 | C. | 0 | D. | -6 |
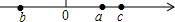 (1)计算:(-2)÷(-2÷$\frac{1}{2}$)-|-3|×(-1)+(-0.5)
(1)计算:(-2)÷(-2÷$\frac{1}{2}$)-|-3|×(-1)+(-0.5)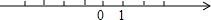 已知在纸面上有一数轴(如图),折叠纸面.
已知在纸面上有一数轴(如图),折叠纸面.