题目内容
3.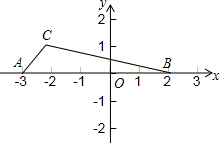 已知A(-3,0),B(2,0),C(-2,1),点D是y轴上的一点.
已知A(-3,0),B(2,0),C(-2,1),点D是y轴上的一点.(1)若A、B、C、D所组成的四边形的面积为15,求D点坐标;
(2)若A、B、C、D所组成的四边形面积小于15,求D点纵坐标的取值范围.
分析 (1)可分别点D在y轴的正半轴上和点D在y轴的负半轴上两种情况计算;
(2)由(1)中点D的坐标可确定出D的取值范围.
解答 解:(1)如图1所示: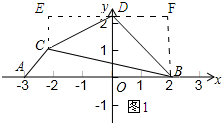
设点D的坐标为(0,m).
∵SABCD=S△ABC+SBCEF-S△CED-S△BDF,
∴$\frac{1}{2}×5×1+\frac{1}{2}(m-1+m)×4$-$\frac{1}{2}×2×(m-1)$-$\frac{1}{2}×2×m$=15.
解得:m=6.75.
如图2所示: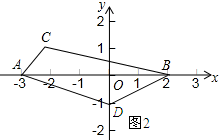
∵SACBD=S△ABC+SABD,
∴$\frac{1}{2}×5×1+\frac{1}{2}×5×(-m)$=15.
解得:m=-5.
综上所述点M的坐标为(0,-5)或(0,6.75).
(2)由(1)可知点D纵坐标的取值范围是-5<Dy<6.75.
点评 本题主要考查的是坐标与图形的性质,根据四边形的面积为15列出关于m的方程是解题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
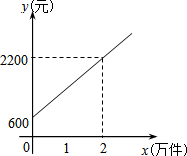 某公司市场营销部的营销员有部分收入按照业务量或销售额提成,即多卖多得.营销员的月提成收入y(元)与其每月的销售量x(万件)成一次函数关系,其图象如图所示.根据图象提供的信息,解答下列问题:
某公司市场营销部的营销员有部分收入按照业务量或销售额提成,即多卖多得.营销员的月提成收入y(元)与其每月的销售量x(万件)成一次函数关系,其图象如图所示.根据图象提供的信息,解答下列问题: 如图,小马虎设计了某个产品的包装盒由于粗心少设计了其中的一部分.请你帮他补上使该图形能折成一个密封的正方体的盒子.
如图,小马虎设计了某个产品的包装盒由于粗心少设计了其中的一部分.请你帮他补上使该图形能折成一个密封的正方体的盒子.