题目内容
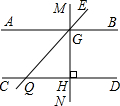 已知,如图,MN⊥AB,垂足为G,MN⊥CD,垂足为H,直线EF分别交AB、CD于G、Q,∠GQC=120°,求∠EGB和∠HGQ的度数.
已知,如图,MN⊥AB,垂足为G,MN⊥CD,垂足为H,直线EF分别交AB、CD于G、Q,∠GQC=120°,求∠EGB和∠HGQ的度数.考点:平行线的判定与性质,垂线
专题:计算题
分析:先根据邻补角的定义得到∠DQG=60°,再根据在同一平面内,垂直于同一条直线的两直线平行得到AB∥CD,根据垂线的定义得∠BGH=90°,然后根据平行线的性质得∠EGB=∠DQG=60°,∠BGQ=∠GQC=120°,则∠HGQ=∠BGQ-∠BGH=30°.
解答:解:∵∠GQC=120°,
∴∠DQG=60°
∵MN⊥AB,MN⊥CD,
∴AB∥CD,∠BGH=90°,
∴∠EGB=∠DQG=60°,∠BGQ=∠GQC=120°,
∴∠HGQ=120°-90°=30°.
∴∠DQG=60°
∵MN⊥AB,MN⊥CD,
∴AB∥CD,∠BGH=90°,
∴∠EGB=∠DQG=60°,∠BGQ=∠GQC=120°,
∴∠HGQ=120°-90°=30°.
点评:本题考查了平行线的判定与性质:在同一平面内,垂直于同一条直线的两直线平行;同位角相等,两直线平行;两直线平行,内错角相等.也考查了垂线的定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
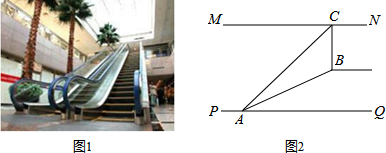
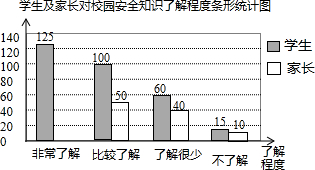 如图所示的两幅不完全的统计图表:
如图所示的两幅不完全的统计图表: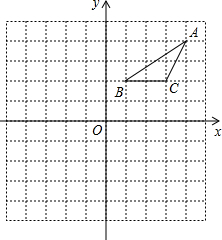 在正方形网格中建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:
在正方形网格中建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:
 如图,AB∥CD∥EF,∠BEF=120°,∠BCD=100°,则∠CBE=
如图,AB∥CD∥EF,∠BEF=120°,∠BCD=100°,则∠CBE=