��Ŀ����
���壺��������y=ax2+bx+c��x�����������Ͷ��㹹��ֱ�������Σ��������������Ϊ��ֱ�������ߡ���
��1��������y=x2-1 ֱ�������ߣ���ǡ����ǡ�����
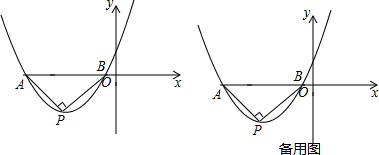
��2����ͼ��ֱ��������y=x2+4x+c��x�ύ�ڵ�A��B��A��B����ࣩ����y�ύ�ڵ�C������ΪP��
����c��ֵ��
����x�����Ƿ���ڵ�Q��ʹ����A��Q��CΪ��������������APB���ƣ������ڣ�
�����Q�����ꣻ�������ڣ���˵�����ɣ�
��3���۲죨1������2���е������߽���ʽ���Բ��룺��ֱ��������y=ax2+bx+c��a��0���У�b2-4ac�Ƿ�Ϊ��ֵ�����ǣ���ֱ��д���ö�ֵ������Ҫ��˵����
��1��������y=x2-1
��2����ͼ��ֱ��������y=x2+4x+c��x�ύ�ڵ�A��B��A��B����ࣩ����y�ύ�ڵ�C������ΪP��
����c��ֵ��
����x�����Ƿ���ڵ�Q��ʹ����A��Q��CΪ��������������APB���ƣ������ڣ�
�����Q�����ꣻ�������ڣ���˵�����ɣ�
��3���۲죨1������2���е������߽���ʽ���Բ��룺��ֱ��������y=ax2+bx+c��a��0���У�b2-4ac�Ƿ�Ϊ��ֵ�����ǣ���ֱ��д���ö�ֵ������Ҫ��˵����

���㣺���κ����ۺ���
ר�⣺
��������1�����ݽ���ʽ�ó�ͼ���������ύ�㣬�����ó���������״��
��2�������ȱ�ʾ��AB�ij��������ó�P�����꣬��AB2=��2PD��2=4PD2�����ɵó�c��ֵ��
�ڣ�����AQC=90�㣬��QA=QCʱ����AQC�ס�APB��������ACQ=90�㣬��CQ=CAʱ�������ó�Q�����ꣻ
��3�����ã�1����2���������b2-4ac��ֵ�����ó��𰸣�
��2�������ȱ�ʾ��AB�ij��������ó�P�����꣬��AB2=��2PD��2=4PD2�����ɵó�c��ֵ��
�ڣ�����AQC=90�㣬��QA=QCʱ����AQC�ס�APB��������ACQ=90�㣬��CQ=CAʱ�������ó�Q�����ꣻ
��3�����ã�1����2���������b2-4ac��ֵ�����ó��𰸣�
��� �⣺��1����������y=x2-1����x�ύ�ڵ㣨1��0������-1��0������������Ϊ����0��-1����
�⣺��1����������y=x2-1����x�ύ�ڵ㣨1��0������-1��0������������Ϊ����0��-1����
�����㹹�ɵ�����������Ϊ��
��
��2��
�ߣ�
��2+��
��2=22��
�����������ֱ�������Σ�
�ʴ�Ϊ���ǣ�
��2������ͼ1����PD��x����D��
��y=0ʱ��x2+4x+c=0��
��ã�x1=-2+
��x2=-2-
��
��AB=x1-x2=2
��
��y=x2+4x+c=��x+2��2+c-4��
��P��-2��c-4����
��4-c��0��
��c��4��
��PD=4-c��
�������ߵĶԳ���֪��PA=PB��
��PD��AB��
��DA=DB��
�ߡ�APB=90�㣬���APB=90�㣬
��AB=2PD��
��AB2=��2PD��2=4PD2��
��4��4-c��=4��4-c��2��
��4-c��0��
��4-c=1��
��c=3��
���ɢ�֪��A��-3��0����B��-1��0����C��0��3����
��OC=OA=3��
�ⷨһ��
�ߡ�APB�ǵ���ֱ�������Σ���Q��x���ϣ�

������AQC=90�㣬��QA=QCʱ����AQC�ס�APB��
��ʱ��Q���O�غϣ�
��Q��0��0����
������ACQ=90�㣬��CQ=CAʱ��
��ACQ�ס�APB��
��ʱ��Q���A����y��Գƣ�
��Q��3��0����
�ⷨ����
�ߡ�CAO=��BAP=45�㣬AP=
��AC=3
��
����
=
ʱ����AQC�ס�APB��

��
=
��
��AQ=3��
��Q��0��0����
����
=
ʱ��
��ACQ�ס�APB��
��
=
��
��AQ=6��
��Q��3��0����
������������x���ϴ��ڵ�Q ��0��0����3��0����ʹ����A��Q��CΪ��������������APB���ƣ�
��3��b2-4ac�Ƕ�ֵ��
��y=x2-1��b2-4ac=4��y=x2+4x+3��b2-4ac=4��
����ֱ��������y=ax2+bx+c��a��0���У�b2-4ac�Ƕ�ֵ��Ϊ4��
 �⣺��1����������y=x2-1����x�ύ�ڵ㣨1��0������-1��0������������Ϊ����0��-1����
�⣺��1����������y=x2-1����x�ύ�ڵ㣨1��0������-1��0������������Ϊ����0��-1���������㹹�ɵ�����������Ϊ��
| 2 |
| 2 |
�ߣ�
| 2 |
| 2 |
�����������ֱ�������Σ�
�ʴ�Ϊ���ǣ�
��2������ͼ1����PD��x����D��
��y=0ʱ��x2+4x+c=0��
��ã�x1=-2+
| 4-c |
| 4-c |
��AB=x1-x2=2
| 4-c |
��y=x2+4x+c=��x+2��2+c-4��
��P��-2��c-4����
��4-c��0��
��c��4��
��PD=4-c��
�������ߵĶԳ���֪��PA=PB��
��PD��AB��
��DA=DB��
�ߡ�APB=90�㣬���APB=90�㣬
��AB=2PD��
��AB2=��2PD��2=4PD2��
��4��4-c��=4��4-c��2��
��4-c��0��
��4-c=1��
��c=3��
���ɢ�֪��A��-3��0����B��-1��0����C��0��3����
��OC=OA=3��
�ⷨһ��
�ߡ�APB�ǵ���ֱ�������Σ���Q��x���ϣ�

������AQC=90�㣬��QA=QCʱ����AQC�ס�APB��
��ʱ��Q���O�غϣ�
��Q��0��0����
������ACQ=90�㣬��CQ=CAʱ��
��ACQ�ס�APB��
��ʱ��Q���A����y��Գƣ�
��Q��3��0����
�ⷨ����
�ߡ�CAO=��BAP=45�㣬AP=
| 2 |
| 2 |
����
| AQ |
| AP |
| AC |
| AB |

��
| AQ | ||
|
3
| ||
| 2 |
��AQ=3��
��Q��0��0����
����
| AQ |
| AB |
| AC |
| AP |
��ACQ�ס�APB��
��
| AQ |
| 2 |
3
| ||
| 2 |
��AQ=6��
��Q��3��0����
������������x���ϴ��ڵ�Q ��0��0����3��0����ʹ����A��Q��CΪ��������������APB���ƣ�
��3��b2-4ac�Ƕ�ֵ��
��y=x2-1��b2-4ac=4��y=x2+4x+3��b2-4ac=4��
����ֱ��������y=ax2+bx+c��a��0���У�b2-4ac�Ƕ�ֵ��Ϊ4��
������������Ҫ�����˶��κ����ۺ��Լ����ɶ��������������ε��ж������ʵ�֪ʶ�����÷������۵ó��ǽ���ؼ���

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
����y=-4x+3��ͼ������������
| A����һ���� | B���ڶ����� |
| C���������� | D���������� |
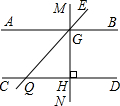 ��֪����ͼ��MN��AB������ΪG��MN��CD������ΪH��ֱ��EF�ֱ�AB��CD��G��Q����GQC=120�㣬���EGB�͡�HGQ�Ķ�����
��֪����ͼ��MN��AB������ΪG��MN��CD������ΪH��ֱ��EF�ֱ�AB��CD��G��Q����GQC=120�㣬���EGB�͡�HGQ�Ķ�����
 ��ͼ��һ��ͼ����һ�룬�������������ͼ���ĶԳ��ᣬ���㻭�����ͼ������һ�룮
��ͼ��һ��ͼ����һ�룬�������������ͼ���ĶԳ��ᣬ���㻭�����ͼ������һ�룮 ��ͼ����ABC�͡�DAE�У���BAC=��DAE��AB=AE��AC=AD������BD��CE����֤����ABD�ա�AEC��
��ͼ����ABC�͡�DAE�У���BAC=��DAE��AB=AE��AC=AD������BD��CE����֤����ABD�ա�AEC��