题目内容
5. 如图,在平面直角坐标系中,已知抛物线y=x2-bx+c经过A(0,3),B(1,0)两点,顶点为M.
如图,在平面直角坐标系中,已知抛物线y=x2-bx+c经过A(0,3),B(1,0)两点,顶点为M.(1)则b=4,c=3;
(2)将△OAB绕点B顺时针旋转90°后,点A落到点C的位置,该抛物线沿y轴上下平移后经过点C,求平移后所得抛物线的表达式.
分析 (1)直接将已知点的坐标代入到二次函数的解析式中求得未知系数的值即可;
(2)根据A、B两点的坐标可以求得OA和OB的长,然后根据旋转的性质求得点C的坐标,然后向下平移2个单位即可得到平移后的抛物线的解析式.
解答 解:(1)已知抛物线y=x2-bx+c经过A(0,3),B(1,0)两点,
∴$\left\{\begin{array}{l}{3=c}\\{0=1-b+c}\end{array}\right.$
解得:$\left\{\begin{array}{l}{b=4}\\{c=3}\end{array}\right.$,
∴b、c的值分别为4,3.
故答案是:4;3.
(2)∵A(0,3),B(1,0),
∴OA=3,OB=1.
∴旋转后C点的坐标为(4,1).
当x=4时,y=x2-4x+3=42-4×4+3=3,
∴抛物线y=x2-4x+3经过点(4,3).
∴将原抛物线沿y轴向下平移2个单位后过点C.
∴平移后的抛物线解析式为y=x2-4x+1.
点评 此题主要考查了函数图象的平移,抛物线与坐标轴的交点坐标的求法,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.会利用方程求抛物线与坐标轴的交点.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
16.$\sqrt{8}$的相反数是( )
| A. | 2$\sqrt{2}$ | B. | -2$\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
13.为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6m3时时,水费按每立方米a元收费,超过6m3时,超过的部分每立方米按c元收费,不超过的部分每立方米仍按a元收费该市某户今年9、10月份的用水量和所交水费如下表所示:
设某户每月用水量x(立方米),应交水费y(元)
(1)a=1.5,c=6;
(2)请分别求出用水不超过6m3和超过6m3时,y与x的函数关系式;
(3)若该户11月份用水8m3,则该户应交水费多少元?
| 月份 | 用水量(m3) | 收费(元) |
| 9 | 5 | 7.5 |
| 10 | 9 | 27 |
(1)a=1.5,c=6;
(2)请分别求出用水不超过6m3和超过6m3时,y与x的函数关系式;
(3)若该户11月份用水8m3,则该户应交水费多少元?
10. 如图,已知AB=CD,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
如图,已知AB=CD,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
 如图,已知AB=CD,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )
如图,已知AB=CD,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )| A. | ∠M=∠N | B. | MB=ND | C. | AM=CN | D. | AM∥CN |
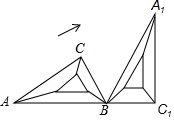 如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针转动一个角度到A1BCl的位置,使得点A,B,C1在同一条直线上,那么这个旋转角的度数等于120°.
如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针转动一个角度到A1BCl的位置,使得点A,B,C1在同一条直线上,那么这个旋转角的度数等于120°.
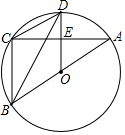 如图,⊙O是△ABC的外接圆,AB为直径,D是⊙O上一点,且OD⊥AC于点E,连结BD、CD.
如图,⊙O是△ABC的外接圆,AB为直径,D是⊙O上一点,且OD⊥AC于点E,连结BD、CD.