题目内容
如图，△ABC中，CD⊥AB于D，E是AC的中点．若AD=6，DE=5，则CD的长等于 ．
8
考点： 勾股定理；直角三角形斜边上的中线．
专题： 计算题．
分析： 由“直角三角形斜边上的中线等于斜边的一半”求得AC=2DE=10；然后在直角△ACD中，利用勾股定理来求线段CD的长度即可．
解答： 解：如图，∵△ABC中，CD⊥AB于D，E是AC的中点，DE=5，
∴DE=
AC=5，
∴AC=10．
在直角△ACD中，∠ADC=90°，AD=6，AC=10，则根据勾股定理，得
CD=
=
=8．
故答案是：8．
点评： 本题考查了勾股定理，直角三角形斜边上的中线．利用直角三角形斜边上的中线等于斜边的一半求得AC的长度是解题的难点．
练习册系列答案
相关题目
，OC=10，O′为△ABC外一点，且△CBO≌△ABO′，则四边形AO′BO的面积为（ ）
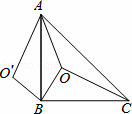
交于点G，AB⊥BE，垂足为B，DE⊥BE，垂足为E，且AB=DE，BF=CE．求证：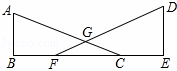
]﹣[
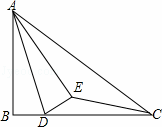
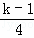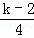]）（符号[a]表示不超过实数a的最大整数，例如[2.6]=2，[0.2]=0），则x2014等于（ ）