Question

如图，点P是∠AOB外的一点，点M，N分别是∠AOB两边上的点，点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在MN的延长线上．若PM=2.5cm，PN=3cm，MN=4cm，则线段QR的长为（　　）

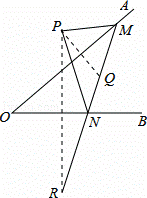
　 A． 4.5cm B． 5.5cm C． 6.5cm D． 7cm

Answer 1

A

考点： 轴对称的性质． 

专题： 几何图形问题．

分析： 利用轴对称图形的性质得出PM=MQ，PN=NR，进而利用MN=4cm，得出NQ的长，即可得出QR的长．

解答： 解：∵点P关于OA的对称点Q恰好落在线段MN上，点P关于OB的对称点R落在MN的延长线上，

∴PM=MQ，PN=NR，

∵PM=2.5cm，PN=3cm，MN=4cm，

∴RN=3cm，MQ=2.5cm，

即NQ=MN﹣MQ=4﹣2.5=1.5（cm），

则线段QR的长为：RN+NQ=3+1.5=4.5（cm）．

故选：A．

点评： 此题主要考查了轴对称图形的性质，得出PM=MQ，PN=NR是解题关键．