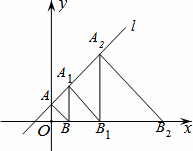题目内容
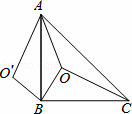
如图，等腰Rt△ABC中，∠ABC=90°，O是△ABC内一点，OA=6，OB=4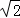
，OC=10，O′为△ABC外一点，且△CBO≌△ABO′，则四边形AO′BO的面积为（ ）
A． 10 B． 16 C． 40 D． 80
C 解：如图，连结OO′．
∵△CBO≌△ABO′，
∴OB=O′B=4
，OC=O′A=10，∠OBC=∠O′BA，
∴∠OBC+∠OBA=∠O′BA+∠OBA，
∴∠O′BO=90°，
∴O′O2=OB2+O′B2=32+32=64，
∴O′O=8．
在△AOO′中，∵OA=6，O′O=8，O′A=10，
∴OA2+O′O2=O′A2，
∴∠AOO′=90°，
∴S四边形AO′BO=S△AOO′+S△OBO′=
×6×8+×4×4=24+16=40．
故选C．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
Rt△A1BB1交直线l于点A1，再过B1点再作等腰Rt△A2B1B2交直线l于点A2，以此类推，继续作等腰Rt△A3B2B3﹣﹣﹣，Rt△AnBn﹣1Bn，其中点A0A1A2…An都在直线l上，点B0B1B2…Bn都在x轴上，且∠A1BB1，∠A2B1B2，∠A3B2B3…∠An﹣1BnBn﹣1都为直角．则点A3的坐标为 ，点An的坐标为 ．
