题目内容
 已知在平面直角坐标系中,点O为坐标原点,过O的直线OM经过点A(6,6),过A作正方形ABCD,在直线OA上有一点E,过E作正方形EFGH,已知直线OC经过点G,且正方形ABCD的边长为2,正方形EFGH的边长为3,则点F的坐标为
已知在平面直角坐标系中,点O为坐标原点,过O的直线OM经过点A(6,6),过A作正方形ABCD,在直线OA上有一点E,过E作正方形EFGH,已知直线OC经过点G,且正方形ABCD的边长为2,正方形EFGH的边长为3,则点F的坐标为考点:一次函数图象上点的坐标特征,正方形的性质
专题:规律型
分析:先利用待定系数法确定直线OA的解析式为y=mx,根据坐标与图形变换由点A(6,6),正方形ABCD的边长为2得到D点坐标为(8,6),C点坐标为(8,4),再利用待定系数法确定直线OC的解析式为y=
x,则可设G点坐标为(t,
t),由于正方形EFGH的边长为3,所以H点坐标为(t,
t+3),从而得到E点坐标为(t-3,
t+3),然后把把E点坐标代入y=x求出t=12,得到E点坐标为(9,9),再把E点向下平移3个单位即可得到F点的坐标.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设直线OA的解析式为y=mx,
把A(6,6)代入得6m=6,解得m=1,
∴直线OA的解析式为y=x,
∵点A(6,6),正方形ABCD的边长为2,
∴D点坐标为(8,6),C点坐标为(8,4).
设直线OC的解析式为y=kx,
把C(8,4)代入y=kx
得8k=4,解得k=
,
∴直线OC的解析式为y=
x,
设G点坐标为(t,
t),
∵正方形EFGH的边长为3,
∴H点坐标为(t,
t+3),E点坐标为(t-3,
t+3),
把E(t-3,
t+3)代入y=x
得t-3=
t+3,解得t=12,
∴E点坐标为(9,9),
∴F点的坐标为(9,6).
故答案为:(9,6).
把A(6,6)代入得6m=6,解得m=1,
∴直线OA的解析式为y=x,
∵点A(6,6),正方形ABCD的边长为2,
∴D点坐标为(8,6),C点坐标为(8,4).
设直线OC的解析式为y=kx,
把C(8,4)代入y=kx
得8k=4,解得k=
| 1 |
| 2 |
∴直线OC的解析式为y=
| 1 |
| 2 |
设G点坐标为(t,
| 1 |
| 2 |
∵正方形EFGH的边长为3,
∴H点坐标为(t,
| 1 |
| 2 |
| 1 |
| 2 |
把E(t-3,
| 1 |
| 2 |
得t-3=
| 1 |
| 2 |
∴E点坐标为(9,9),
∴F点的坐标为(9,6).
故答案为:(9,6).
点评:本题考查了一次函数的性质与正方形的性质,会运用待定系数法确定一次函数解析式;理解坐标与图形变换.

练习册系列答案
相关题目
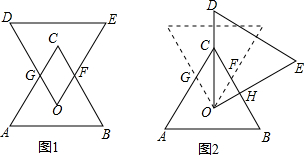 如图(1),有两个全等的正三角形ABC和ODE,点O、C分别为△ABC、△DEO的重心;固定点O,将△ODE顺时针旋转,使得OD经过点C,如图(2),则图(2)中四边形OGCF与△OCH面积的比为
如图(1),有两个全等的正三角形ABC和ODE,点O、C分别为△ABC、△DEO的重心;固定点O,将△ODE顺时针旋转,使得OD经过点C,如图(2),则图(2)中四边形OGCF与△OCH面积的比为