题目内容
8.若x-y=6,y-z=5,求x2+y2+z2-xy-xz-yz的值.分析 由x-y=6,y-z=5易得x-z=11,然后把x2+y2+z2-xy-yz-xz进行变形得到$\frac{1}{2}$(2x2+2y2+2z2-2xy-2yz-2xz),根据完全平方公式分组分解为$\frac{1}{2}$[(x-y)2+(y-z)2+(x-z)2],再代值计算即可.
解答 解:∵x-y=6,y-z=5,
∴x-z=11,
∴x2+y2+z2-xy-yz-xz
=$\frac{1}{2}$(2x2+2y2+2z2-2xy-2yz-2xz)
=$\frac{1}{2}$[(x-y)2+(y-z)2+(x-z)2]
=$\frac{1}{2}$(62+52+112)
=91.
点评 此题考查因式分解的实际运用,掌握完全平方公式:(a±b)2=a2±2ab+b2是解决问题的关键.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案
相关题目
19.下列各式的恒等变形属于分解因式的是( )
| A. | (x+2)(x-2)=x2-4 | B. | x2-9+x=(x+3)(x-3)+x | ||
| C. | 3x2-5x=2x(x-2)+x2-x | D. | x2-2xy+y2=(x-y)2 |
13.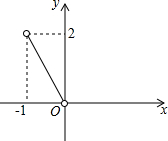 已知函数图象如图所示,则此函数解析式为( )
已知函数图象如图所示,则此函数解析式为( )
 已知函数图象如图所示,则此函数解析式为( )
已知函数图象如图所示,则此函数解析式为( )| A. | y=-2x | B. | y=-2x(-1<x<0) | C. | y=-$\frac{1}{2}$x | D. | y=-$\frac{1}{2}$x(-1<x<0) |
18.下列说法中,正确的是( )
| A. | 两个角为直角的四边形是矩形 | |
| B. | 有一组对边相等,一组对角是直角的四边形是矩形 | |
| C. | 一组对边平行,一个角是直角的四边形是矩形 | |
| D. | 两条对角线垂直且相等的四边形是矩形 |
 如图所示,AB=AC=12,BC=7,AB的垂直平分线交AB于D,交AC于F,求△BCE的周长.
如图所示,AB=AC=12,BC=7,AB的垂直平分线交AB于D,交AC于F,求△BCE的周长.