题目内容
如图,已知:在平行四边形ABCD中,点E、F、G、H分别在边AB、BC、CD、DA上,AE=CG,AH=CF,且EG平分∠HEF.求证:
(1)△AEH≌△CGF;
(2)四边形EFGH是菱形.
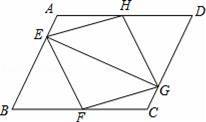

【考点】平行四边形的性质;全等三角形的判定与性质;菱形的判定.
【专题】证明题.
【分析】(1)由全等三角形的判定定理SAS证得结论;
(2)易证四边形EFGH是平行四边形,那么EF∥GH,那么∠HGE=∠FEG,而EG是角平分线,易得∠HEG=∠FEG,根据等量代换可得∠HEG=∠HGE,从而有HE=HG,易证四边形EFGH是菱形.
【解答】(1)证明:如图,∵四边形ABCD是平行四边形,
∴∠A=∠C,
在△AEH与△CGF中,
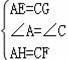
 ,
,
∴△AEH≌△CGF(SAS);
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D.
又∵AE=CG,AH=CF,
∴BE=DG,BF=DH,
在△BEF与△DGH中,
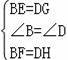

∴△BEF≌△DGH(SAS),
∴EF=GH.
又由(1)知,△AEH≌△CGF,
∴EH=GF,
∴四边形EFGH是平行四边形,
∴HG∥EF,
∴∠HGE=∠FEG,
∵EG平分∠HEF,
∴∠HEG=∠FEG,
∴∠HEG=∠HGE,
∴HE=HG,
∴四边形EFGH是菱形.


【点评】本题考查了全等三角形的判定和性质、平行四边形的判定和性质、菱形的判定.解题的关键是掌握两组对边相等的四边形是平行四边形,一组邻边相等的平行四边形是菱形.

练习册系列答案
相关题目



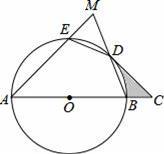
 ,BC=2,以AB为直径的⊙O分别交AC、BC两边于点D、E,则△CDE的面积为 .
,BC=2,以AB为直径的⊙O分别交AC、BC两边于点D、E,则△CDE的面积为 .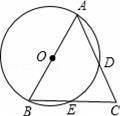


 =
=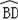
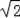


 米,则这个坡面的坡度为( )
米,则这个坡面的坡度为( )

 ,计算:
,计算:

 )﹣1的值.
)﹣1的值.