题目内容
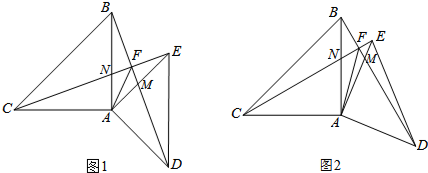
如图,已知△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC,AD=AE.连接 BD交AE于M,连接CE交AB于N,BD与CE交点为F,连接AF.
(1)如图1,求证:BD⊥CE;
(2)如图1,求证:FA是∠CFD的平分线;
(3)如图2,当AC=2,∠BCE=15°时,求CF的长.
(1)如图1,求证:BD⊥CE;
(2)如图1,求证:FA是∠CFD的平分线;
(3)如图2,当AC=2,∠BCE=15°时,求CF的长.

考点:全等三角形的判定与性质,勾股定理,等腰直角三角形
专题:
分析:(1)根据SAS即可求得△CAE≌△BAD,求得∠ACF=∠ABD.因为∠ANC=∠BNF,根据三角形的内角和定理就可求得∠BFN=∠NAC=90°,从而证得BD⊥CE;
(2)作AG⊥CE于G,AK⊥BD于K.根据三角形面积公式即可求得AG=AK.根据角的平分线的性质定理的逆定理即可证得FA是∠CFD的平分线;
(3)根据已知条件求得∠ACN=∠ACB-∠BCE=30°=∠FBN.在Rt△ACN中,通过解直角三角形从而求得AN=
,CN=
.进而求得BN=2-
. 在Rt△ACN中通过解直角三角形求得NF=
BN=
.即可求得CF=CN+NF=1+
.
(2)作AG⊥CE于G,AK⊥BD于K.根据三角形面积公式即可求得AG=AK.根据角的平分线的性质定理的逆定理即可证得FA是∠CFD的平分线;
(3)根据已知条件求得∠ACN=∠ACB-∠BCE=30°=∠FBN.在Rt△ACN中,通过解直角三角形从而求得AN=
2
| ||
| 3 |
4
| ||
| 3 |
2
| ||
| 3 |
| 1 |
| 2 |
3-
| ||
| 3 |
| 3 |
解答: (1)证明:如图1.
(1)证明:如图1.
∵∠BAC=∠DAE=90°,∠BAE=∠BAE,
∴∠CAE=∠BAD.
在△CAE和△BAD中,
,
∴△CAE≌△BAD(SAS),
∴∠ACF=∠ABD.
∵∠ANC=∠BNF,
∴∠BFN=∠NAC=90°.
∴BD⊥CE.
(2)证明:如图1,作AG⊥CE于G,AK⊥BD于K.
由(1)知△CAE≌△BAD,
∴CE=BD,S△CAE=S△BAD,
∴AG=AK.
∴点A在∠CFD的平分线上.
即 FA是∠CFD的平分线.
(3)如图2.
∵∠BAC=90°,AB=AC,
∴∠ACB=∠ABC=45°.
∵∠BCE=15°,
∴∠ACN=∠ACB-∠BCE=30°=∠FBN.
在Rt△ACN中
∵∠NAC=90°,AC=2,∠ACN=30°,
∴AN=
,CN=
.
∵AB=AC=2,
∴BN=2-
.
在Rt△ACN中
∵∠BFN=90°,∠FBN=30°,
∴NF=
BN=
.
∴CF=CN+NF=1+
.
 (1)证明:如图1.
(1)证明:如图1.∵∠BAC=∠DAE=90°,∠BAE=∠BAE,
∴∠CAE=∠BAD.
在△CAE和△BAD中,
|
∴△CAE≌△BAD(SAS),
∴∠ACF=∠ABD.
∵∠ANC=∠BNF,
∴∠BFN=∠NAC=90°.
∴BD⊥CE.
(2)证明:如图1,作AG⊥CE于G,AK⊥BD于K.
由(1)知△CAE≌△BAD,
∴CE=BD,S△CAE=S△BAD,
∴AG=AK.
∴点A在∠CFD的平分线上.
即 FA是∠CFD的平分线.
(3)如图2.

∵∠BAC=90°,AB=AC,
∴∠ACB=∠ABC=45°.
∵∠BCE=15°,
∴∠ACN=∠ACB-∠BCE=30°=∠FBN.
在Rt△ACN中
∵∠NAC=90°,AC=2,∠ACN=30°,
∴AN=
2
| ||
| 3 |
4
| ||
| 3 |
∵AB=AC=2,
∴BN=2-
2
| ||
| 3 |
在Rt△ACN中
∵∠BFN=90°,∠FBN=30°,
∴NF=
| 1 |
| 2 |
3-
| ||
| 3 |
∴CF=CN+NF=1+
| 3 |
点评:本题考查了等腰直角三角形的性质,全等三角形的判定,角的平分线的判定等知识点,利用全等三角形得出线段相等和角相等是解题的关键.

练习册系列答案
相关题目
在平面直角坐标系中,点(-4,5)关于原点对称的点的坐标为( )
| A、(4,-5) |
| B、(4,5) |
| C、(-4,-5) |
| D、(-4,5) |
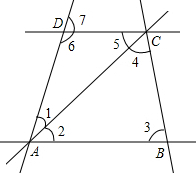 如图所示,从标有数字的角中找出:
如图所示,从标有数字的角中找出: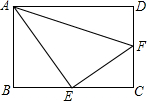 已知:如图,矩形ABCD中,点E是BC的中点,点F在CD上,AE是∠BAF的角平分线.
已知:如图,矩形ABCD中,点E是BC的中点,点F在CD上,AE是∠BAF的角平分线.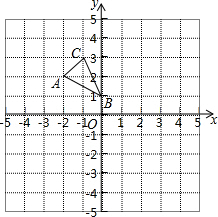 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(0,1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(0,1). 在△ABC中,AB=9,AC=5,AD是∠BAC的平分线交BC于点D(如图),△ABD沿直线AD翻折后,点B落到点B1处,如果∠B1DC=
在△ABC中,AB=9,AC=5,AD是∠BAC的平分线交BC于点D(如图),△ABD沿直线AD翻折后,点B落到点B1处,如果∠B1DC=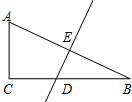 在Rt△ABC中,∠BCA=90°,AB的垂直平分线交BC与点D,若AB=8,BD=5,则CD=
在Rt△ABC中,∠BCA=90°,AB的垂直平分线交BC与点D,若AB=8,BD=5,则CD=