题目内容
在同一直角坐标系中画出二次函数y=
x2+1与二次函数y=-
x2-1的图形.
(1)从抛物线的开口方向、形状、对称轴、顶点等方面说出两个函数图象的相同点与不同点;
(2)说出两个函数图象的性质的相同点与不同点.
| 1 |
| 3 |
| 1 |
| 3 |
(1)从抛物线的开口方向、形状、对称轴、顶点等方面说出两个函数图象的相同点与不同点;
(2)说出两个函数图象的性质的相同点与不同点.
考点:二次函数的图象
专题:
分析:根据二次函数图象,可得二次函数的性质.
解答:解:如图:
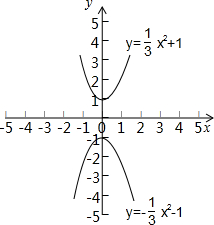 ,
,
(1)y=
x2+1与y=-
x2-1的相同点是:形状都是抛物线,对称轴都是y轴,
y=
x2+1与y=-
x2-1的不同点是:y=
x2+1开口向上,顶点坐标是(0,1),y=-
x2-1开口向下,顶点坐标是(0,-1);
(2)性质的相同点:开口程度相同,不同点:y=
x2+1 当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大;
y=-
x2-1当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小.
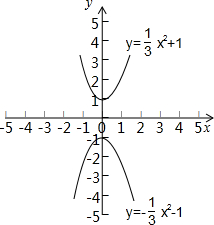 ,
,(1)y=
| 1 |
| 3 |
| 1 |
| 3 |
y=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
(2)性质的相同点:开口程度相同,不同点:y=
| 1 |
| 3 |
y=-
| 1 |
| 3 |
点评:本题考查了二次函数的图象,利用了二次函数图象与性质,a>0图象开口向上,对称轴左侧,y随x的增大而减小,对称轴右侧,y随x的增大而增大;a<0图象开口向下,对称轴左侧,y随x的增大而增大,对称轴右侧,y随x的增大而减小.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )
如图,每个小正方形的边长为1,A、B、C是小正方形的顶点,则∠ABC的度数为( )| A、30゜ | B、45゜ |
| C、60゜ | D、90゜ |
 如图,AB=AC,AD=AE,则图中全等的三角形的对数共有( )对.
如图,AB=AC,AD=AE,则图中全等的三角形的对数共有( )对.| A、2对 | B、3对 | C、4对 | D、5对 |
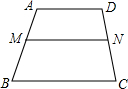 如图,在梯形ABCD中AD∥BC,点M为腰AB上的一点,MN∥BC交DC于点N,MN与AD是否平行?请说明理由,分别测量出点MN到BC的距离,两者有何关系.
如图,在梯形ABCD中AD∥BC,点M为腰AB上的一点,MN∥BC交DC于点N,MN与AD是否平行?请说明理由,分别测量出点MN到BC的距离,两者有何关系.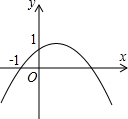 如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(-1,0),下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>-1时,y>0.其中正确结论的个数是:
如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(-1,0),下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>-1时,y>0.其中正确结论的个数是: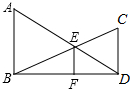 已知,如图所示,AB∥CD,AD交BC于点E,EF∥AB交BD于点F.
已知,如图所示,AB∥CD,AD交BC于点E,EF∥AB交BD于点F. 棱长为a的正方体摆放成如图的形状:
棱长为a的正方体摆放成如图的形状: