题目内容
7. 如图所示,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$的解集是x<-1.
如图所示,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$的解集是x<-1.
分析 根据直线y=ax+b交x轴于点(4,0),直线y=cx+d交x轴于点(-1,0),再结合图象即可得出两不等式的解集,进而得出答案.
解答 解:∵直线y=ax+b交x轴于点(4,0),
∴ax+b>0的解集为:x<4,
∵直线y=cx+d交x轴于点(-1,0),
∴cx+d<0的解集为:x<-1,
∴不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$的解集是:x<-1.
故答案为:x<-1.
点评 本题考查了一次函数与一元一次不等式,属于基础题,关键是正确根据图象解题.

练习册系列答案
相关题目
2.若※是新规定的运算符号,设a※b=a2-ab,则3※12的值是( )
| A. | -6 | B. | -3 | C. | 15 | D. | -27 |
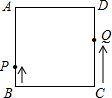 已知正方形ABCD中,AB=BC=CD=AD=10cm,动点P,Q分别从点B,C同时出发沿正方形的四周运动.设点P的运动速度为2cm/s,点Q的运动速度为3cm/s,设点P,Q运动的时间为t(s)
已知正方形ABCD中,AB=BC=CD=AD=10cm,动点P,Q分别从点B,C同时出发沿正方形的四周运动.设点P的运动速度为2cm/s,点Q的运动速度为3cm/s,设点P,Q运动的时间为t(s)
 如图,一张长方形桌子的桌面长100cm,宽60cm,一块长方形台布的面积是桌面面积是2$\frac{3}{4}$倍,并且铺在桌面上时,各边垂下的长度相等,求台布的长和宽.
如图,一张长方形桌子的桌面长100cm,宽60cm,一块长方形台布的面积是桌面面积是2$\frac{3}{4}$倍,并且铺在桌面上时,各边垂下的长度相等,求台布的长和宽. 列方程解应用题.
列方程解应用题.