题目内容
12.(1)$\sqrt{8}$+$\sqrt{32}$-$\sqrt{2}$;(2)$\frac{10\sqrt{2}-\sqrt{98}}{\sqrt{2}}$;
(3)$\sqrt{12}$+$\sqrt{\frac{1}{27}}$-$\sqrt{\frac{1}{3}}$;
(4)$\sqrt{12}$+|$\sqrt{3}$-2|+(2-π)0;
(5)($\sqrt{7}$+$\sqrt{3}$)($\sqrt{7}$-$\sqrt{3}$)-$\sqrt{16}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先把各二次根式化为最简二次根式,然后合并后进行二次根式的除法运算;
(3)先把各二次根式化为最简二次根式,然后合并即可;
(4)利用绝对值和零指数幂的意义计算;
(5)利用平方差公式计算.
解答 解:(1)原式=2$\sqrt{2}$+4$\sqrt{2}$-$\sqrt{2}$
=5$\sqrt{2}$;
(2)原式=$\frac{10\sqrt{2}-7\sqrt{2}}{\sqrt{2}}$
=3;
(3)原式=2$\sqrt{3}$-$\frac{\sqrt{3}}{9}$-$\frac{\sqrt{3}}{3}$
=$\frac{14\sqrt{3}}{9}$;
(4)原式=2$\sqrt{3}$+2-$\sqrt{3}$+1
=$\sqrt{3}$+3;
(5)原式=7-3-4
=0.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂和负整数指数幂.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
2.某洗衣机厂本周计划每日生产400台洗衣机,由于人数和操作原因,每日实际分别生产405台,393台,397台,410台,391台,385台,405台.
(1)用正负数表示每日实际生产量与计划量的增减情况,并完成下面表格.
(2)该洗衣机厂本周实际生产多少台洗衣机?平均每日实际生产多少台洗衣机?
(1)用正负数表示每日实际生产量与计划量的增减情况,并完成下面表格.
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | 5台 | -7台 | -3台 | 10台 | -9台 | -15台 | 5台 |
2. 画如图所示物体的俯视图,正确的是( )
画如图所示物体的俯视图,正确的是( )
 画如图所示物体的俯视图,正确的是( )
画如图所示物体的俯视图,正确的是( )| A. |  | B. |  | C. |  | D. |  |
 如图、矩形ABCD中,AB=8,AD=6.点M是对角线AC上的一个动点,以M点为圆心,线段AM长为半径画一个⊙M,若⊙M在以C为端点的矩形ABCD边上截得的线段EF=$\frac{6}{5}$AM,则线段AM的长是$\frac{30}{7}$或5.
如图、矩形ABCD中,AB=8,AD=6.点M是对角线AC上的一个动点,以M点为圆心,线段AM长为半径画一个⊙M,若⊙M在以C为端点的矩形ABCD边上截得的线段EF=$\frac{6}{5}$AM,则线段AM的长是$\frac{30}{7}$或5. 已知△ABC分别作出∠ACB的角平分线,BC边上的中线和AC边上的高.(要求:用尺规作图,并写出已知、求作,保留作图痕迹,不写作法.)
已知△ABC分别作出∠ACB的角平分线,BC边上的中线和AC边上的高.(要求:用尺规作图,并写出已知、求作,保留作图痕迹,不写作法.) 如图所示,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$的解集是x<-1.
如图所示,可以得出不等式组$\left\{\begin{array}{l}{ax+b>0}\\{cx+d<0}\end{array}\right.$的解集是x<-1. 如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的负半轴上,点C在y轴的正半轴上,OA=5,OC=4,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.
如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的负半轴上,点C在y轴的正半轴上,OA=5,OC=4,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D、E两点的坐标.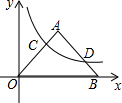 如图,双曲线y=$\frac{k}{x}$在第一象限内的图象与等腰直角三角形OAB相交于C点和D点,∠A=90°,OA=1,OC=2BD,则k的值是$\frac{8}{25}$.
如图,双曲线y=$\frac{k}{x}$在第一象限内的图象与等腰直角三角形OAB相交于C点和D点,∠A=90°,OA=1,OC=2BD,则k的值是$\frac{8}{25}$.