题目内容
15.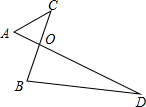 如图,AD与BC相交于点O,$\frac{OA}{OB}$=$\frac{OC}{OD}$,且OA=2,OB=AC=3,求BD的长.
如图,AD与BC相交于点O,$\frac{OA}{OB}$=$\frac{OC}{OD}$,且OA=2,OB=AC=3,求BD的长.
分析 根已知条件可以判定△AOC∽△BOD,利用相似三角形的对应边成比例进行解答.
解答  解:∵如图,AD与BC相交于点O,$\frac{OA}{OB}$=$\frac{OC}{OD}$,∠AOC=∠BOD,
解:∵如图,AD与BC相交于点O,$\frac{OA}{OB}$=$\frac{OC}{OD}$,∠AOC=∠BOD,
∴△AOC∽△BOD,
∴$\frac{OA}{OB}$=$\frac{AC}{BD}$,即$\frac{2}{3}$=$\frac{3}{BD}$.
则BD=4.5.
点评 本题考查了相似三角形的判定与性质.三角形相似的判定一直是中考考查的热点之一,在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边以及对顶角等隐含条件.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
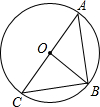 如图所示,点O为⊙O的圆心,则线段OA,OB,OC是圆O的半径,线段AB,BC,AC是圆O的弦,其中最长的弦是AC,$\widehat{AB}$,$\widehat{BC}$,是劣弧.
如图所示,点O为⊙O的圆心,则线段OA,OB,OC是圆O的半径,线段AB,BC,AC是圆O的弦,其中最长的弦是AC,$\widehat{AB}$,$\widehat{BC}$,是劣弧.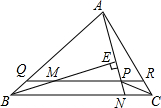 如图,过△ABC的顶点A,作直线AE与∠B的内角平分线垂直相交于点E,且与∠C的内角平分线相交于点P,过P作直线与底边BC平行,且与AB交于Q,与AC交于R,求证:QR=AQ+CR.
如图,过△ABC的顶点A,作直线AE与∠B的内角平分线垂直相交于点E,且与∠C的内角平分线相交于点P,过P作直线与底边BC平行,且与AB交于Q,与AC交于R,求证:QR=AQ+CR.