题目内容
19.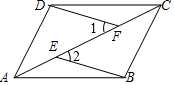 如图,在四边形ABCD中,AD∥BC,E、F是对角线AC上的两点,AE=CF,∠1=∠2,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,AD∥BC,E、F是对角线AC上的两点,AE=CF,∠1=∠2,求证:四边形ABCD是平行四边形.
分析 证出AF=CE,由ASA证明△ADF≌△CBE,得出AD=BC,即可得出四边形ABCD是平行四边形.
解答 证明:∵AD∥BC,
∴∠DAF=∠BCE,
∵AE=CF,
∴AE+EF=CF+EF,
即AF=CE,
∵∠1=∠2,
在△ADF和△CBE中,$\left\{\begin{array}{l}{∠DAF=∠BCE}&{\;}\\{AF=CE}&{\;}\\{∠1=∠2}&{\;}\end{array}\right.$,
∴△ADF≌△CBE(ASA),
∴AD=BC,
∴四边形ABCD是平行四边形.
点评 本题考查了平行四边形的判定、全等三角形的判定与性质;证明三角形全等是解决问题的关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
9.若等边三角形的一条高为$\sqrt{3}$,其边长为( )
| A. | 2 | B. | 1 | C. | 3 | D. | D、 |
10.下列说法正确的是( )
| A. | 相等的两个角是对顶角 | |
| B. | 同位角相等 | |
| C. | 图形平移后的大小可以发生改变 | |
| D. | 两条直线相交所成的四个角都相等,则这两条直线互相垂直 |
 已知甲、乙两地相距90km,A、B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE、OC分别表示A、B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题:
已知甲、乙两地相距90km,A、B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE、OC分别表示A、B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题: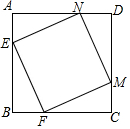 如图,E,F,M,N分别是边长为4的正方形ABCD四条边上的点,且AE=BF=CM=DN.那么四边形EFMN的面积的最小值是8.
如图,E,F,M,N分别是边长为4的正方形ABCD四条边上的点,且AE=BF=CM=DN.那么四边形EFMN的面积的最小值是8.