Question

12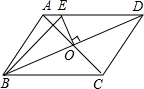．如图，平行四边形ABCD的周长为20cm，对角线相交于点O，且EO⊥BD于点O交AD于E，则△ABE的周长为10cm．

Answer 1

分析 利用线段垂直平分线的性质即可求出BE=DE，得出△ABE的周长=AB+AE+BE=AB+AD．

解答 解：∵AC，BD相交于点O，
∴O为BD的中点，
∵OE⊥BD，
∴BE=DE，
△ABE的周长=AB+AE+BE=AB+AD=$\frac{1}{2}$×20=10（cm），
故答案为：10．

点评 本题考查的是平行四边形的性质及线段垂直平分线的性质，解答此题的关键是将三角形的三边长转为平行四边形的一组邻边的长的和．