题目内容
某饮料厂生产一种饮料,经测算,用1吨水生产的饮料所获利润y(元)是1吨水的价格x(元)的一次函数.
(1)根据表中提供的数据,求y与x的函数关系式;当水价为每吨20元时,1吨水生产出的饮料所获的利润是多少?
(2)为节约用水,这个市规定:该厂日用水量不超过20吨时,水价为每吨4元;日用水量超过20吨时,超过部分按每吨40元收费.已知该厂日用水量不少于20吨,设该厂日用水量为t吨,当日所获利润为W元.求W与t的函数关系式;该厂加强管理,积极节水,使日用水量不超过25吨,但仍不少于20吨,求该厂的日利润的取值范围.
| 1吨水的价格x(元) | 6 | 8 |
| 用1吨水生产的饮料所获利润(元) | 198 | 196 |
(2)为节约用水,这个市规定:该厂日用水量不超过20吨时,水价为每吨4元;日用水量超过20吨时,超过部分按每吨40元收费.已知该厂日用水量不少于20吨,设该厂日用水量为t吨,当日所获利润为W元.求W与t的函数关系式;该厂加强管理,积极节水,使日用水量不超过25吨,但仍不少于20吨,求该厂的日利润的取值范围.
考点:一次函数的应用,二元一次方程组的应用
专题:
分析:(1)用1吨水生产的饮料所获利润y(元)是1吨水的价格x(元)的一次函数.可以设出一次函数关系式,然后根据表中所给的条件(6,198)(8,196)可求出解析式;
(2)根据函数式可求出一吨水价是40的利润,然后根据题意可得w=200×20+164(t-20),代入t=20或t=25可求出日利润的取值范围.
(2)根据函数式可求出一吨水价是40的利润,然后根据题意可得w=200×20+164(t-20),代入t=20或t=25可求出日利润的取值范围.
解答:解:(1)用1吨水生产的饮料所获利润y(元)是1吨水的价格x(元)的一次函数式为
根据题意得:y=kx+b,
,
解得
,
故所求一次函数式是y=-x+204,
当x=20时,y=-20+204=184(元);
(2)当1吨水的价格为40元时,所获利润是:y=-40+204=164(元).
∴W与t的函数关系式是w=200×20+(t-20)×164,
即w=164t+720,
∵20≤t≤25,
∴4000≤w≤4820.
根据题意得:y=kx+b,
|
解得
|
故所求一次函数式是y=-x+204,
当x=20时,y=-20+204=184(元);
(2)当1吨水的价格为40元时,所获利润是:y=-40+204=164(元).
∴W与t的函数关系式是w=200×20+(t-20)×164,
即w=164t+720,
∵20≤t≤25,
∴4000≤w≤4820.
点评:本题考查的是用一次函数解决实际问题,注意利用一次函数求最值时,关键是应用一次函数的性质;即由函数y随x的变化,结合自变量的取值范围确定最值.

练习册系列答案
相关题目
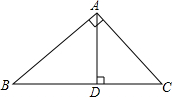 如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD:CD=3:2,则
如图,Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若BD:CD=3:2,则| AD |
| BD |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
要得到y=-2(x+2)2-3的图象,需将抛物线y=-2x2作如下平移( )
| A、向右平移2个单位,再向上平移3个单位 |
| B、向右平移2个单位,再向下平移3个单位 |
| C、向左平移2个单位,在向下平移3个单位 |
| D、向左平移2个单位,再向下平移3个单位 |
36°18′等于( )
| A、36.6° |
| B、36.3° |
| C、36.1° |
| D、36.2° |
三条互不重合的直线的交点个数可能是( )
| A、0,1,3 |
| B、0,2,3 |
| C、0,1,2,3 |
| D、0,1,2 |
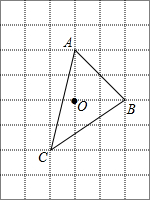 如图:
如图: 如图,在△ABC中,AB=AC=
如图,在△ABC中,AB=AC=