题目内容
5. 如图,AB=AC,点D,E分别为AB和AC的中点,CD,BE相交于点O,求证:∠B=∠C.
如图,AB=AC,点D,E分别为AB和AC的中点,CD,BE相交于点O,求证:∠B=∠C.
分析 根据中点的性质和AB=AC证明AD=AE,根据三角形全等的判定定理证明△ABE≌△ACD,根据全等三角形的性质证明结论.
解答 证明:∵点D,E分别为AB和AC的中点,
∴AD=$\frac{1}{2}$AB,AE=$\frac{1}{2}$AC,又AB=AC,
∴AD=AE,
在△ABE和△ACD中,
$\left\{\begin{array}{l}{AD=AE}\\{∠A=∠A}\\{AC=AB}\end{array}\right.$,
∴△ABE≌△ACD,
∴∠B=∠C.
点评 本题考查的是三角形全等的判定和性质,灵活运用全等三角形的判定定理和性质定理是解题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
13.如果一次函数y=kx+b的图象经过第二象限内一点,且与y轴负半轴相交,那么( )
| A. | k<0,b<0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k>0,b>0 |
10.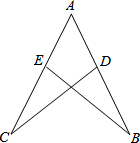 如图,增加条件能判断△ACD≌△ABE的是( )
如图,增加条件能判断△ACD≌△ABE的是( )
 如图,增加条件能判断△ACD≌△ABE的是( )
如图,增加条件能判断△ACD≌△ABE的是( )| A. | AC=AB,AD=AE | B. | ∠AEB=∠ADC | C. | AC=AB,CD=BE | D. | ∠C=∠B |
17.若a2-2a+1+|b-2|=0,则以a、b为边长的等腰三角形的周长为( )
| A. | 4 | B. | 5 | C. | 4或5 | D. | 无法确定 |
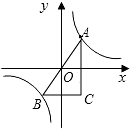 如图,点A(2,y)是反比例函数y=$\frac{12}{x}$的图象上一点,延长AO交该图象于点B,AC⊥x轴,BC⊥y轴,求△ABC的面积.
如图,点A(2,y)是反比例函数y=$\frac{12}{x}$的图象上一点,延长AO交该图象于点B,AC⊥x轴,BC⊥y轴,求△ABC的面积. 实数a、b、c在数轴上的位置如图所示,化简:$\sqrt{(a-b)^{2}}$-|a+c|+$\sqrt{(c-b)^{2}}$-|-2b|.
实数a、b、c在数轴上的位置如图所示,化简:$\sqrt{(a-b)^{2}}$-|a+c|+$\sqrt{(c-b)^{2}}$-|-2b|.