题目内容
数列x1,x2,…,x100满足下列条件:对于k=1,2,…,100,xk比其余99个数的和小k,已知x50=
,m,n是互质的正整数,则m+n等于( )
| m |
| n |
| A、50 | B、100 |
| C、165 | D、173 |
考点:整数问题的综合运用
专题:计算题
分析:根据xk比其余99个数的和小k,可得出k+2xk=S,然后将k的值依次代入求和可得出S的值,也可得出m+n的值.
解答:解:设S=x1+x2+…x100,则xk=(S-xk)-k,即k+2xk=S,
故可得:1+2x1=S,2+2x2=S,3+2x3=S,4+2x4=S,…,100+2x100=S,
将各式求和得:(1+2+…+100)+2S=100S,
解得:S=
,
故x50=
=
,
求得m+n=173.
故选D.
故可得:1+2x1=S,2+2x2=S,3+2x3=S,4+2x4=S,…,100+2x100=S,
将各式求和得:(1+2+…+100)+2S=100S,
解得:S=
| 2525 |
| 49 |
故x50=
| S-50 |
| 2 |
| 75 |
| 98 |
求得m+n=173.
故选D.
点评:此题考查了整数问题的综合运用,解答本题的关键是根据题意得出关系式k+2xk=S,这是本题的突破口,有一定难度.

练习册系列答案
相关题目
已知⊙O1和⊙O2的半径分别为6和2,O1O2=3,则⊙O1和⊙O2的位置关系是( )
| A、相交 | B、外离 | C、内含 | D、内切 |
 如图,正△ABC内接于⊙O,动点P在圆周的劣弧AB上,且不与A、B重合,则∠BPC=( )
如图,正△ABC内接于⊙O,动点P在圆周的劣弧AB上,且不与A、B重合,则∠BPC=( )| A、60° | B、30° |
| C、90° | D、120° |
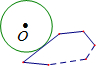 如图,⊙O沿凸n边形的外侧(圆和边相切)无滑动地滚动一周回到原来的位置,当⊙O和凸n边形的周长相等时,那么⊙O自身转动了( )圈.
如图,⊙O沿凸n边形的外侧(圆和边相切)无滑动地滚动一周回到原来的位置,当⊙O和凸n边形的周长相等时,那么⊙O自身转动了( )圈.
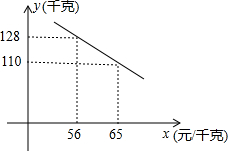 千克)与销售单价x(元/千克)关系如图所示,解答下列问题:
千克)与销售单价x(元/千克)关系如图所示,解答下列问题: