题目内容
6.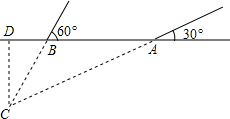 2014年3月,某海域发生航班失联事件,我海事救援部门用高频海洋探测仪进行海上搜救,分别在A、B两个探测点探测到C处是信号发射点,已知A、B两点相距400m,探测线与海平面的夹角分别是30°和60°,若CD的长是点C到海平面的最短距离.
2014年3月,某海域发生航班失联事件,我海事救援部门用高频海洋探测仪进行海上搜救,分别在A、B两个探测点探测到C处是信号发射点,已知A、B两点相距400m,探测线与海平面的夹角分别是30°和60°,若CD的长是点C到海平面的最短距离.(1)问BD与AB有什么数量关系,试说明理由;
(2)求信号发射点的深度.(结果精确到1m,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
分析 (1)易证三角形ABC的是等腰三角形,再根据30°所对直角边是斜边的一半可求出DB的长,
(2)由(1)结合勾股定理即可求出CD的长.
解答 解:(1)由图形可得∠BCA=30°,
∴CB=BA=400米,
∴在Rt△CDB中又含30°角,得DB=$\frac{1}{2}$CB=200米,
可知,BD=$\frac{1}{2}$AB,
(2)由勾股定理DC=$\sqrt{{CB}^{2}-{BD}^{2}}$
=$\sqrt{{400}^{2}-{200}^{2}}$,
=200$\sqrt{3}$米,
∴点C的垂直深度CD是346米.
点评 本题考查了解直角三角形的应用,难度适中,解答本题的关键是构造直角三角形,解直角三角形,也考查了把实际问题转化为数学问题的能力.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
16.若三角形的一个外角小于和它相邻的内角,则这个三角形为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
1.已知等腰△ABC中,AD⊥BC于点D,且AD=$\frac{1}{2}$BC,则△ABC底角的度数为( )
| A. | 45° | B. | 75° | C. | 45°或15°或75° | D. | 60° |
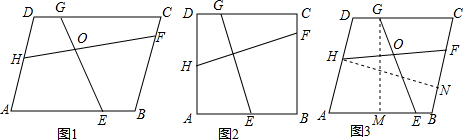
 小明在拼图时发现,用8个一样大的长方形恰好可以拼成一个大的长方形,如图1所示;小红看见了,说:“我来试一试!”结果小红七拼八凑,拼成了一个如图2所示的正方形,但中间留下了一个洞,恰好是边长为2mm的小正方形.则每个小长方形的长是10mm,宽是6mm.
小明在拼图时发现,用8个一样大的长方形恰好可以拼成一个大的长方形,如图1所示;小红看见了,说:“我来试一试!”结果小红七拼八凑,拼成了一个如图2所示的正方形,但中间留下了一个洞,恰好是边长为2mm的小正方形.则每个小长方形的长是10mm,宽是6mm.
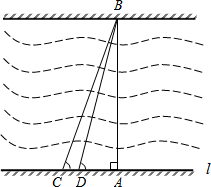 某市为了改善市区交通状况,计划在康富路的北端修建通往资江北岸的新大桥,如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.
某市为了改善市区交通状况,计划在康富路的北端修建通往资江北岸的新大桥,如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.