题目内容
18.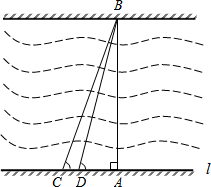 某市为了改善市区交通状况,计划在康富路的北端修建通往资江北岸的新大桥,如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.
某市为了改善市区交通状况,计划在康富路的北端修建通往资江北岸的新大桥,如图,新大桥的两端位于A、B两点,小张为了测量A、B之间的河宽,在垂直于新大桥AB的直线型道路l上测得如下数据:∠BDA=76.1°,∠BCA=68.2°,CD=82米.求:AB的长(精确到0.1米,参考数据:sin76.1°≈0.97,cos76.1°≈0.24,tan76.1°≈4.0;sin68.2°≈0.93,cos68.2°≈0.37,tan68.2°≈2.5).
分析 在Rt△ABC中,AC=$\frac{AB}{tan68.2°}$,在Rt△ABD中,AD=$\frac{AB}{tan76.1°}$,再根据AC-AD=82,即可解答.
解答 解:在Rt△ABC中,AC=$\frac{AB}{tan68.2°}$,
在Rt△ABD中,AD=$\frac{AB}{tan76.1°}$,
AC-AD=$\frac{AB}{tan68.2°}$-$\frac{AB}{tan76.1°}$=82,
解之得,AB≈546.7米.
点评 本题考查了解直角三角形的应用,用三角函数表示出AC、AD的长,再相减即为CD的长.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
7.四边形剪掉一个角后,变为( )边形.
| A. | 3 | B. | 4 | C. | 5 | D. | 3或4或5 |
13.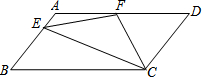 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF=$\frac{1}{2}$∠BCD,(2)EF=CF;(3)S△BEC=2S△CEF;(4)∠DFE=3∠AEF,其中正确结论的个数是( )
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF=$\frac{1}{2}$∠BCD,(2)EF=CF;(3)S△BEC=2S△CEF;(4)∠DFE=3∠AEF,其中正确结论的个数是( )
 如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF=$\frac{1}{2}$∠BCD,(2)EF=CF;(3)S△BEC=2S△CEF;(4)∠DFE=3∠AEF,其中正确结论的个数是( )
如图,在?ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF=$\frac{1}{2}$∠BCD,(2)EF=CF;(3)S△BEC=2S△CEF;(4)∠DFE=3∠AEF,其中正确结论的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.下列说法正确的是( )
| A. | -$\frac{x{y}^{2}}{5}$的系数是-5 | B. | $\frac{t}{2}$是分式 | ||
| C. | $\frac{\sqrt{2}}{2}$不是分数 | D. | -22xyz2的次数是6 |
7.若某数a增加它的x%后得到b,则b等于( )
| A. | a+x% | B. | (1+x%)a | C. | a(1+x)% | D. | a•x% |
 如图,△ABC中,∠C=90°,∠1=∠2,BC=6cm,DC=2$\sqrt{3}$cm,求AB、AC的长.
如图,△ABC中,∠C=90°,∠1=∠2,BC=6cm,DC=2$\sqrt{3}$cm,求AB、AC的长.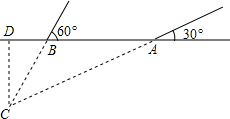 2014年3月,某海域发生航班失联事件,我海事救援部门用高频海洋探测仪进行海上搜救,分别在A、B两个探测点探测到C处是信号发射点,已知A、B两点相距400m,探测线与海平面的夹角分别是30°和60°,若CD的长是点C到海平面的最短距离.
2014年3月,某海域发生航班失联事件,我海事救援部门用高频海洋探测仪进行海上搜救,分别在A、B两个探测点探测到C处是信号发射点,已知A、B两点相距400m,探测线与海平面的夹角分别是30°和60°,若CD的长是点C到海平面的最短距离.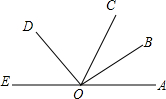 如图,已知OB是∠AOC平分线,OD是∠COE平分线,∠COD=2∠AOB.
如图,已知OB是∠AOC平分线,OD是∠COE平分线,∠COD=2∠AOB.