题目内容
17.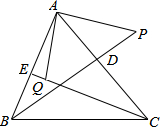 如图,BD,CE分别是△ABC的边AC,AB上的高线,点P在BD的延长线上,BP=AC;点Q在CE上,CQ=BA,猜想AP和AQ的关系,并证明你的猜想.
如图,BD,CE分别是△ABC的边AC,AB上的高线,点P在BD的延长线上,BP=AC;点Q在CE上,CQ=BA,猜想AP和AQ的关系,并证明你的猜想.
分析 根据垂直的定义得到∠AEC=90,∠ADB=90,通过△ABP≌△QCA,根据全等三角形的性质得到AP=AQ,由于∠P+∠PAD=90°,∠P=∠CAQ,于是得到∠QAC+∠PAD=90°,故可得出结论.
解答 解:猜想:AP⊥AQ且AP=AQ;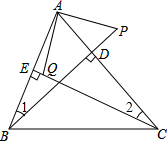
证明:∵BD,CE是△ABC的高,
∴∠AEC=∠ADB=90°,
∴∠1+∠BAC=90°,∠2+∠BAC=90°,
∴∠1=∠2.
在△ABP与△QCA中,
$\left\{\begin{array}{l}{AB=CQ}\\{∠1=∠2}\\{BP=AC}\end{array}\right.$,
∴△ABP≌△QCA(SAS),
∴AP=AQ,∠P=∠QAC,
又∵∠P+∠PAD=90°,
∴∠QAC+∠PAD=90°,即AP⊥AQ,
∴AP⊥AQ且AP=AQ.
点评 本题考查的是全等三角形的判定与性质,熟知全等三角形的SAS、ASA及SSS定理是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
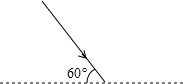 如图,与水平方向成60°角的入射光,我们想利用平面镜使它沿水平方向射向远处,请你画出符合要求的光路图表达你的想法,并标出镜面与水平方向的夹角.
如图,与水平方向成60°角的入射光,我们想利用平面镜使它沿水平方向射向远处,请你画出符合要求的光路图表达你的想法,并标出镜面与水平方向的夹角.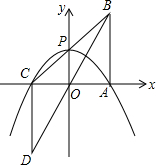 如图,已知△OAB的顶点坐标分别是0(0,0),A(1,0),B(1,2).将△OAB绕点O按逆时针方向旋转180°得到△OCD.
如图,已知△OAB的顶点坐标分别是0(0,0),A(1,0),B(1,2).将△OAB绕点O按逆时针方向旋转180°得到△OCD.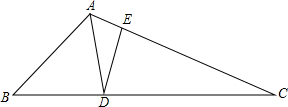 如图,已知△ABC,AD平分∠BAC,DE垂直AC,垂足为E,∠ADB=2∠B=4∠C,AE=$\frac{3}{4}$,CD=$\frac{7}{2}$,则线段AB=$\frac{55}{26}$.
如图,已知△ABC,AD平分∠BAC,DE垂直AC,垂足为E,∠ADB=2∠B=4∠C,AE=$\frac{3}{4}$,CD=$\frac{7}{2}$,则线段AB=$\frac{55}{26}$.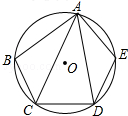 如图,在圆的内接五边形ABCDE中,∠B+∠E=220°,则∠CAD=40°.
如图,在圆的内接五边形ABCDE中,∠B+∠E=220°,则∠CAD=40°.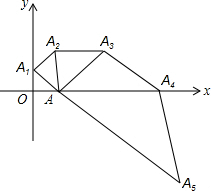 如图,已知△OAA1是腰长为1的等腰直角三角形,以Rt△OAA1的斜边AA1为直角边,画第二个等腰Rt△AA1A2,再以Rt△AA1A2为直角边,画第三个等腰Rt△AA2A3,…,以此类推,则点A2016的坐标是[-21008+1,($\sqrt{2}$)2015 ]..
如图,已知△OAA1是腰长为1的等腰直角三角形,以Rt△OAA1的斜边AA1为直角边,画第二个等腰Rt△AA1A2,再以Rt△AA1A2为直角边,画第三个等腰Rt△AA2A3,…,以此类推,则点A2016的坐标是[-21008+1,($\sqrt{2}$)2015 ]..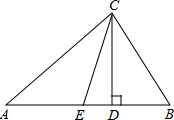 如图,在△ABC中,CD、CE分别是△ABC的高和角平分线.
如图,在△ABC中,CD、CE分别是△ABC的高和角平分线.