题目内容
2.已知二次函数y=kx2+(2k-1)x-1与x轴交点的横坐标为x1、x2(x1<x2),则对于下列结论:①当x>x1时,y>0;
②方程kx2+(2k-1)x-1=0有两个不相等的实数根x1、x2;
③x1<-1,x2>-1;
④x2-x1=$\frac{\sqrt{1+4{k}^{2}}}{k}$,
其中正确的结论是( )
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
分析 ①二次项系数k不确定,不知道开口方向不能确定;②二次函数与x轴的交点,即转换为一元二次方程等于0的解;③利用根与系数的关系可知(x1+1)(x2+1)<0,从而可求得答案;④两根相减需确定二次项系数的符号.
解答 解:①因不知道k的符号,就不知道开口方向,无法确定,错误;
②因二次函数y=kx2+(2k-1)x-1与x轴有两个交点,所以,方程kx2+(2k-1)x-1=0有两个不相等的实数根x1、x2,正确;
③∵(x1+1)(x2+1)=x1x2+x1+x2+1=-$\frac{1}{k}$-$\frac{2k-1}{k}$+1=-1<0,又x1<x2,
∴x1+1<x2+1,x1+1<0,x2+1>0,即x1<-1,x2>-1,正确;
④因为k的符号不确定,无法知道x2-x1的大小,错误.
∴正确的结论是②③.
故选:B.
点评 主要考查了二次函数的性质、一元二次方程的根、以及根与系数之间的关系,利用根与系数的关系得到(x1+1)(x2+1)<0是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.下列图形不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
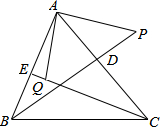 如图,BD,CE分别是△ABC的边AC,AB上的高线,点P在BD的延长线上,BP=AC;点Q在CE上,CQ=BA,猜想AP和AQ的关系,并证明你的猜想.
如图,BD,CE分别是△ABC的边AC,AB上的高线,点P在BD的延长线上,BP=AC;点Q在CE上,CQ=BA,猜想AP和AQ的关系,并证明你的猜想. 如图,折叠长方形纸片ABCD,先折出折痕(对角线)BD,在折叠,使AD落在对角线BD上,得折痕DG,若AB=2,BC=1,求AG.
如图,折叠长方形纸片ABCD,先折出折痕(对角线)BD,在折叠,使AD落在对角线BD上,得折痕DG,若AB=2,BC=1,求AG.